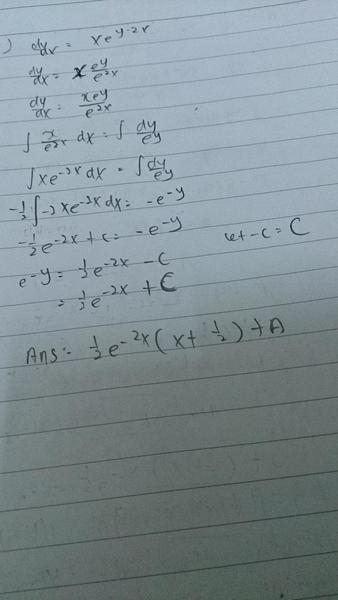SUMMARY
The discussion centers on the differential equation dy/dx = xe^(y-2x) and the process of forming a solution. The provided answer is (e^-y) = 0.5(e^-2x)(x+0.5) + a, indicating that the task involves solving the differential equation rather than merely forming it. Participants emphasize the importance of verifying integration steps, particularly the integration of 2x e^(2x), to ensure accuracy in deriving the solution.
PREREQUISITES
- Understanding of differential equations
- Knowledge of integration techniques
- Familiarity with exponential functions
- Ability to differentiate functions
NEXT STEPS
- Review methods for solving first-order differential equations
- Study integration techniques for exponential functions
- Learn about the application of integrating factors in differential equations
- Explore the verification of solutions through differentiation
USEFUL FOR
Students studying calculus, mathematics enthusiasts, and anyone looking to deepen their understanding of differential equations and their solutions.