Solve this problem that involves implicit differentiation

[chwala]

Homework Statement

See attached question and ms

Relevant Equations

differentiation

The question and ms guide is pretty much clear to me. I am attempting to use a non-implicit approach.

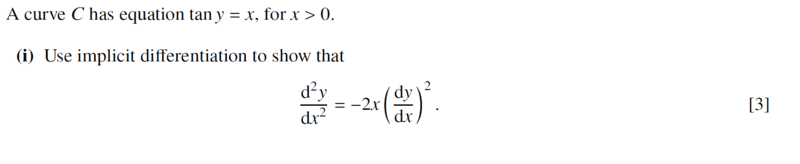
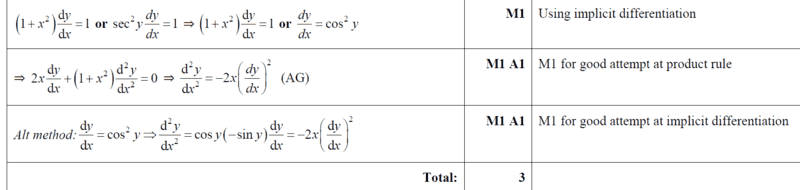$\tan y=x, ⇒y=\tan^{-1} x$
We know that $1+ \tan^2 x= \sec^2 x$
$\dfrac{dx}{dy}=sec^2 y$
$\dfrac{dx}{dy}=1+\tan^2 y$
$\dfrac{dy}{dx}=\dfrac{1}{1+x^2}$
$\dfrac{d^2y}{dx^2}=\dfrac{(1+x)0-1(2x)}{(1+x^2)^2}$
$\dfrac{d^2y}{dx^2}=\dfrac{-2x}{(1+x^2)^2}$
$\dfrac{d^2y}{dx^2}=-2x ⋅\left(\dfrac{dx}{dy}\right)^2$

No question here ...just looking at the problem from a different perspective ...any insight is welcome...

 

[Mark44]

$\dfrac{dx}{dy}=sec^2 y$
$\dfrac{dx}{dy}=1+\tan^2 y$
$\dfrac{dy}{dx}=\dfrac{1}{1+x^2}$
$\dfrac{d^2y}{dx^2}=\dfrac{(1+x)0-1(2x)}{(1+x^2)^2}$

Typo in the line above, but it doesn't affect the subsequent work. The first product in the numerator should be $(1 + x^2)0$.

$\dfrac{d^2y}{dx^2}=\dfrac{-2x}{(1+x^2)^2}$
$\dfrac{d^2y}{dx^2}=-2x ⋅\left(\dfrac{dx}{dy}\right)^2$

No question here ...just looking at the problem from a different perspective ...any insight is welcome...

 

[chwala]

Typo in the line above, but it doesn't affect the subsequent work. The first product in the numerator should be $(1 + x^2)0$.

Argggggh @Mark44 ... let me grab some coffee now. Cheers mate.

 

[Office_Shredder]

All this flipping of x and y is confusing, not just for the reader but for you too (your final result has dx/dy instead of dy/dx).

I would suggest not trying to modify the equation. Just differentiate $tan(y)=x$ with respect to $x$, then do it again, then try to substitute all the trig functions for other things you know the value of.

 

[chwala]

All this flipping of x and y is confusing, not just for the reader but for you too (your final result has dx/dy instead of dy/dx).

I would suggest not trying to modify the equation. Just differentiate $tan(y)=x$ with respect to $x$, then do it again, then try to substitute all the trig functions for other things you know the value of.

Let me amend that...thanks...

$\tan y=x, ⇒y=\tan^{-1} x$
We know that $1+ \tan^2 x= \sec^2 x$
$\dfrac{dx}{dy}=sec^2 y$
$\dfrac{dx}{dy}=1+\tan^2 y$
$\dfrac{dy}{dx}=\dfrac{1}{1+x^2}$
$\dfrac{d^2y}{dx^2}=\dfrac{(1+x^2)0-1(2x)}{(1+x^2)^2}$
$\dfrac{d^2y}{dx^2}=\dfrac{-2x}{(1+x^2)^2}$
$\dfrac{d^2y}{dx^2}=-2x ⋅\left(\dfrac{dy}{dx}\right)^2$

 

[Delta2]

The way I would solve it is what is coined as "Alt" method in the picture. (Which has a typo too btw, the second equation should be $$\frac{d^2y}{dx^2}=2\cos y(-\sin y)\frac{dy}{dx}$$.

 

[Office_Shredder]

No, you're still missing the point. Your first step really looks like you don't see the point of implicit differentiation. If you're going to solve for y as a function of x, you might as well just do normal differentiation.

$\frac{d}{dx} \tan(y)=1$

Compute that, and differentiate again

 

[Delta2]

No, you're still missing the point. Your first step really looks like you don't see the point of implicit differentiation. If you're going to solve for y as a function of x, you might as well just do normal differentiation.

$\frac{d}{dx} \tan(y)=1$

Compute that, and differentiate again

He is mentioning in the OP that he is going to use a non implicit differentiation method (thus ignoring the problem statement prompt).

 

[chwala]

No, you're still missing the point. Your first step really looks like you don't see the point of implicit differentiation. If you're going to solve for y as a function of x, you might as well just do normal differentiation.

$\frac{d}{dx} \tan(y)=1$

Compute that, and differentiate again

@Office_Shredder i understand implicit differentiation very well...as easy as {a,b,c}...I was looking at normal differentiation...

 

[chwala]

The way I would solve it is what is coined as "Alt" method in the picture. (Which has a typo too btw, the second equation should be $$\frac{d^2y}{dx^2}=2\cos y(-\sin y)\frac{dy}{dx}$$.

Interesting that a 'Further Maths' Marks scheme would have an error or typo...

 

[Delta2]

well when you implicitly differentiate $cos^2y$ you get $$2\cos y\frac{d\cos y}{dx}$$, its clearly a typo.

 

[chwala]

well when you implicitly differentiate $cos^2y$ you get $$2\cos y\frac{d\cos y}{dx}$$, its clearly a typo.

yeah...just looking at the implicit part again...is there a simple way of showing $x=\cos y ⋅siny?$
As In the Implicit approach we shall have,

$tan y=x$

$sec^2 y \dfrac{dy}{dx} =1$

$\dfrac{dy}{dx}=cos^2y$

$\dfrac{d^2y}{dx^2}=-2\cos y\sin y \dfrac{dy}{dx}$

$\dfrac{d^2y}{dx^2}=-2\left[\dfrac{1}{\sqrt(1+x^2)} ⋅\dfrac{x}{\sqrt(1+x^2)}\right]\dfrac{dy}{dx}=-2x⋅\left[ \dfrac{1}{1+x^2}\right]\dfrac{dy}{dx}=-2x⋅\dfrac{dy}{dx}⋅\dfrac{dy}{dx}=-2x\left(\dfrac{dy}{dx}\right)^2$

 

[Delta2]

It is $$x\frac{dy}{dx}=\cos y\sin y$$ actually. And yes it is not so straightforward but not very hard either. To reach to this, start from $$\frac{\sin y}{\cos y}=x$$ and multiply both sides by $\cos^2y=\frac{dy}{dx}$

 

[Delta2]

Typo again in your work (also you use a mix of implicit and explicit methods), the final result has the first derivative squared!

 

[SammyS]

yeah...just looking at the implicit part again...is there a simple way of showing $x=\cos y ⋅siny?$
As In the Implicit approach we shall have,

$tan y=x$

$sec^2 y \dfrac{dy}{dx} =1$

$\dfrac{dy}{dx}=cos^2y$

$\dfrac{d^2y}{dx^2}=-2\cos y\sin y \dfrac{dy}{dx}$

$\dfrac{d^2y}{dx^2}=-2\left[\dfrac{1}{\sqrt(1+x^2)} ⋅\dfrac{x}{\sqrt(1+x^2)}\right]\dfrac{dy}{dx}=-2x⋅\left[ \dfrac{1}{1+x^2}\right]\dfrac{dy}{dx}=-2x⋅\dfrac{dy}{dx}⋅\dfrac{dy}{dx}=-2x\left(\dfrac{dy}{dx}\right)^2$

Notice that $\displaystyle -2\cos y\sin y \dfrac{dy}{dx}=-2\cos^2y \dfrac{\sin y}{\cos y}\dfrac{dy}{dx}$

$\displaystyle \quad\quad\quad\quad\quad\quad=-2\cos^2y \tan y\dfrac{dy}{dx}$

$\displaystyle \quad\quad\quad\quad\quad\quad=-2 ~~ \dfrac{dy}{dx}\quad x \quad \dfrac{dy}{dx}$

 

[chwala]

Notice that $\displaystyle -2\cos y\sin y \dfrac{dy}{dx}=-2\cos^2y \dfrac{\sin y}{\cos y}\dfrac{dy}{dx}$

$\displaystyle \quad\quad\quad\quad\quad\quad=-2\cos^2y \tan y\dfrac{dy}{dx}$

$\displaystyle \quad\quad\quad\quad\quad\quad=-2 ~~ \dfrac{dy}{dx}\quad x \quad \dfrac{dy}{dx}$

eeeeeeish @SammyS smart there!

I was just looking at the biography of Paul Erdos! "Is your brain open?" What a Legend! A real Mathematician!