Dynamics - Lagrange's Equations

[Andrew85]

Hi, revising for my christmas exams and am really struggling to get my bearing with Lagrangian Equations. I think its just the initial steps that I can't seem to follow.
This is a tutorial question that I just can't get my head around:

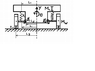
Use Lagrange’s Equations to obtain the equations of motion of the vehicle model shown, about the equilibrium position. The vehicle is symmetrical about the vertical centre line and you may assume small displacements and hence neglect any lateral movements of the masses, spring ends and link pivots.
Note: L1 = (L2 + L3)/2 i.e. the spring is attached half way along the link and the links attaching the wheels to the body are horizontal ( φ1 = φ2 = 0 ) at the equilibriumposition shown. Also, because we are interested in motion about the equilibriumposition it is not necessary to take into account any change in gravitational potential energy associated with the motion of the masses.

There should be a pic of the problem attached. Thanks for any help on how to get started.

 

[AlephZero]

The first thing to do is decide what your generalized variables are. Looking at the picture, they are Y, theta, theta_1, theta_2 with the sign conventions shown by the arrows.

Then work out the kinetic and potential energy of each part of the structure in terms of the generalized variables.

E.g. the right hand wheel has velocity (upwards) Ydot + L3 theta-dot - (L3-L2) theta1-dot. Write the KE = 1/2.Mw.v^2 as a matrix expression like

1/2 [Ydot thetadot theta1dot theta2dot]Transposed . [A symmetric 4x4 matrix with Ms and Ls in it] . [Ydot thetadot theta1dot theta2dot].

Repeat for the other parts of the structire - add all the KE terms for the different parts into the same 4x4 matrix of course.

The PE is very similar except using displacements not velocities.

Lagrangian dynamics is a great tool, provided somebody else has set up the equations of motion already, before you get to work on the problem :-(

Hope that helps you get going.

 

[piercas]

Hello, it sounds like you are struggling with understanding the initial steps of using Lagrange's equations. I will try to provide some guidance to help you get started on this problem.

First, let's review what Lagrange's equations are and how they are used. Lagrange's equations are a set of equations that describe the motion of a system of particles. They are derived from the principle of least action, which states that the actual motion of a system is the one that minimizes the action (a quantity that takes into account the energy and forces acting on the system).

To use Lagrange's equations, we need to define a set of generalized coordinates that uniquely describe the configuration of the system. In this problem, the generalized coordinates would be the angles φ1 and φ2, which describe the rotation of the two masses about the equilibrium position. We also need to define a Lagrangian function, which is a function of the generalized coordinates and their time derivatives. The Lagrangian represents the total energy of the system.

Now, let's apply this to the problem at hand. We have a vehicle with two masses, two springs, and two links. The vehicle is symmetrical and we are only interested in small displacements, so we can neglect any lateral movements. This means that the only forces acting on the system are the spring forces and the gravitational forces. We can also assume that the gravitational potential energy remains constant because we are only interested in motion about the equilibrium position.

To obtain the equations of motion, we need to first write out the Lagrangian function. This can be done by considering the kinetic energy and potential energy of the system. The kinetic energy is given by 1/2*m*v^2, where m is the mass and v is the velocity. In this case, the velocity of each mass can be expressed in terms of the generalized coordinates and their time derivatives using basic trigonometry. The potential energy is given by the spring potential energy, which is 1/2*k*x^2, where k is the spring constant and x is the displacement of the spring from its equilibrium position. Again, the displacements can be expressed in terms of the generalized coordinates.

Once we have the Lagrangian function, we can use Lagrange's equations to obtain the equations of motion. These equations are given by d/dt(∂L/∂q̇) - ∂L/∂q = Q, where L is