Trying2Learn
- 375
- 57
Summary:: Can someone point me to an example solution?
Hello
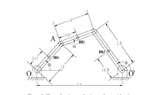
The attached figure is a four bar link. Each of the four bars has geometry, mass, moment of inertia, etc.
A torque motor drives the first link.
I am looking for an example (a simple solution so I can ground my self before exploring more complicated situations), of using Hamilton's Principle with a loop closure constraint.
I do not even know how to begin.
Well, I can formulate the kinetic energy and potential energy of the bars. I can account for the applied non-conservative torque ( but bringing it in through Principle of Virtual work). I can do that... for a NON-closed link.
But I would prefer to do the closed loop by bringing in constraint equations. I can write the constraint equation on the position and another set on the velocities, but I have no idea how to append those constraints to the Lagrangian, or even the final output (From the calculus of variations) that leads to the Euler Lagrange equations.
Can someone start me off?
EDIT: in fact, I cannot even begin. Do I use Lagrange multipliers for the position constraint? AND the velocity constraint? Or just one of the two. I cannot even begin.
In fact, I do not even know how to state the question... this is the best I can do:
How do I append the Lagrangian (or the final Euler Lagrange equation sets) for a four bar link, when the loop is closed and I have the loop closure equations for position and velocity. Is that even stated correctly ?
Hello
The attached figure is a four bar link. Each of the four bars has geometry, mass, moment of inertia, etc.
A torque motor drives the first link.
I am looking for an example (a simple solution so I can ground my self before exploring more complicated situations), of using Hamilton's Principle with a loop closure constraint.
I do not even know how to begin.
Well, I can formulate the kinetic energy and potential energy of the bars. I can account for the applied non-conservative torque ( but bringing it in through Principle of Virtual work). I can do that... for a NON-closed link.
But I would prefer to do the closed loop by bringing in constraint equations. I can write the constraint equation on the position and another set on the velocities, but I have no idea how to append those constraints to the Lagrangian, or even the final output (From the calculus of variations) that leads to the Euler Lagrange equations.
Can someone start me off?
EDIT: in fact, I cannot even begin. Do I use Lagrange multipliers for the position constraint? AND the velocity constraint? Or just one of the two. I cannot even begin.
In fact, I do not even know how to state the question... this is the best I can do:
How do I append the Lagrangian (or the final Euler Lagrange equation sets) for a four bar link, when the loop is closed and I have the loop closure equations for position and velocity. Is that even stated correctly ?
Attachments
Last edited: