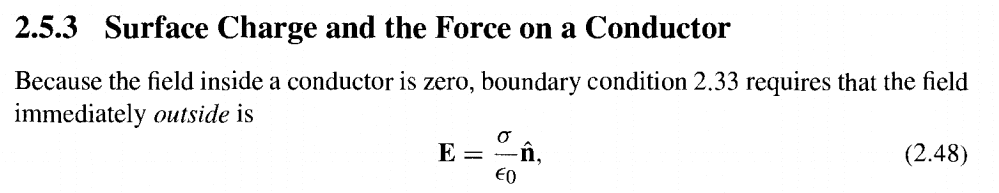Discussion Overview
The discussion revolves around the behavior of the electric field (E-field) immediately outside a charged conductor, particularly in the context of Gauss's law and surface charge density. Participants explore theoretical implications, clarify concepts, and address confusion regarding the application of established results to different geometries of conductors.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- One participant expresses confusion about Griffith's assertion regarding the E-field immediately outside a charged conductor and questions whether E would equal zero when using a Gaussian surface that does not enclose the inducing charge.
- Another participant initially misreads the question but later acknowledges the need to disregard their previous comment.
- Some participants discuss the implications of the conductor being uncharged overall, noting that while the integral of the E-field over a closed surface may be zero, this does not imply that the E-field itself is zero outside the conductor.
- There is a clarification that the normal component of the E-field changes by an amount equal to the surface charge density divided by the permittivity of free space (σ/ε₀) at any discontinuity, regardless of the conductor's shape.
- One participant questions the applicability of the result E = σ/ε₀n_hat to finite conductors, suggesting it may only apply to infinite planes.
- A response addresses the concept of "infinite" in this context, explaining that it refers to a conductor being very large relative to the distance from its surface, and that the boundary condition holds for finite conductors when observed from a sufficiently small distance.
Areas of Agreement / Disagreement
Participants exhibit some agreement on the behavior of the E-field near charged conductors, particularly regarding the change in the normal component of the field. However, there remains disagreement and confusion about the applicability of certain results to finite versus infinite conductors, indicating that the discussion is not fully resolved.
Contextual Notes
Participants note that the concept of "infinite" is context-dependent and relates to the scaling distance compared to the local radius of curvature of the conductor. The discussion highlights the importance of understanding the conditions under which certain theoretical results apply.