KDPhysics
- 73
- 24
Summary:: Not sure if my solution to a magnetostatics problem is correct
[Mentor Note -- thread moved from the technical forums, so no Homework Template is shown]
I was trying to solve problem 2 from: https://ocw.mit.edu/courses/physics/8-022-physics-ii-electricity-and-magnetism-fall-2006/exams/exam2.pdf
Here is my solution:
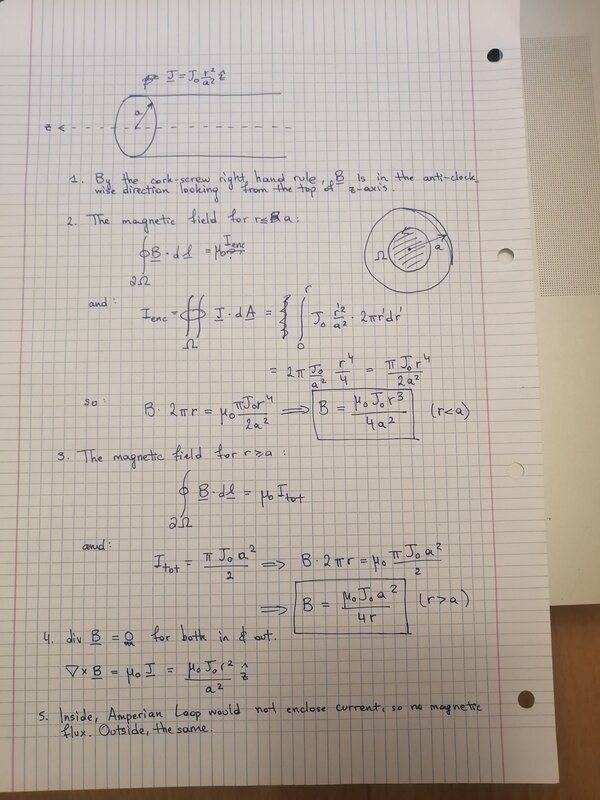
[Mentor Note -- thread moved from the technical forums, so no Homework Template is shown]
I was trying to solve problem 2 from: https://ocw.mit.edu/courses/physics/8-022-physics-ii-electricity-and-magnetism-fall-2006/exams/exam2.pdf
Here is my solution:
Last edited by a moderator: