E&M: Forces resulting from Charges at the Corners of a Cube

[cherry]

Homework Statement

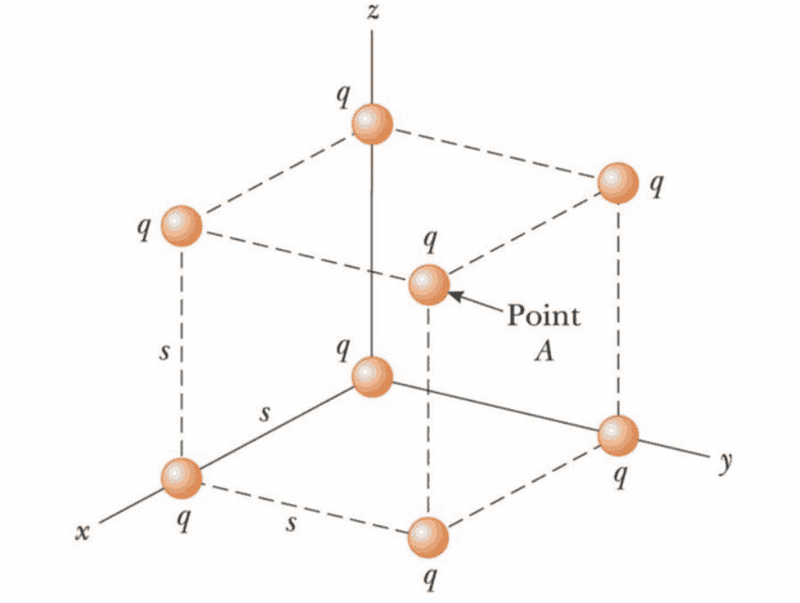
Eight point charges, each of magnitude q =4.76e-06 C, are located on the corners of a cube of edge s=14.8 cm, as shown in the figure. What is the magnitude of the resultant force exerted by the other charges on the charge located at point A? Image: https://drive.google.com/file/d/1mOFCbEIpWz8IohRbg-ZmnU2rn6VfZ7dS/view?usp=sharing

Relevant Equations

F=k*(q^2/r^2)

My first attempt at solving:

I divided up the point charges based on the radius away from point A.
1 charge was s*sqrt(3) away, 3 charges were s*sqrt(2) away, and 3 charges were s away from point A.
q remained constant.

Therefore, my F_total was:
F_total = k * [(q^2 / s^2*sqrt(3))+3(q^2/s^2*sqrt(2))+3(q^2/s^2)]

When I solved this, I got the wrong answer, unfortunately.
Can someone lead me in the right direction?

 

[PeroK]

Force is a vector. The magnitude of a sum of vectors is not the sum of the magnitudes.

 

[Orodruin]

Apart from what was already said, I would notice that all components (x, y, and z) must be equal due to the symmetry of the problem. It is therefore sufficient to compute one of the components, which may be slightly faster.

 

[cherry]

Hi, I tried that and got 64.427 as my answer which was unfortunately wrong.

Unless I made a calculation error, in which case, could you let me know where the error is?

 

[PeroK]

I get that three charges do not contribute to the force in the x-direction:

 

[Steve4Physics]

Hi @cherry. A few comments...

The Post #1 diagram shows point A at (s, s, s). But the Post #4 diagram shows it at (0, 0, s). So make sure you know which one is correct. And you seem to have renamed the charge on which the total force is required as 'K' to add to the confusion!

To perform the correct vector adiditions, you need to add the x components of all forces on A to get the x component of the total force on A; similary for y and z components. Then you combine these to get the total magnitude. So make sure you are correctly resolving each force into its x, y and z components.

Note that your answer of '64.427', even if it were correct, would lose you 2 marks: 1 mark for an inappropriate number of significant figures and 1 mark for missing units.

And if you can take-on @Orodruin's and @PeroK's replies, you can save yourself a lot of work.

Edit: typo's.

 

[cherry]

Hi @cherry. A few comments...

The Post #1 diagram shows point A at (s, s, s). But the Post #4 diagram shows it at (0, 0, s). So make sure you know which one is correct. And you seem to have renamed the charge on which the total force is required as 'K' to add to the confusion!

To perform the correct vector adiditions, you need to add the x components of all forces on A to get the x component of the total force on A; similary for y and z components. Then you combine these to get the total magnitude. So make sure you are correctly resolving each force into its x, y and z components.

Note that your answer of '64.427', even if it were correct, would lose you 2 marks: 1 mark for an inappropriate number of significant figures and 1 mark for missing units.

And if you can take-on @Orodruin's and @PeroK's replies, you can save yourself a lot of work.

Edit: typo's.

Hi, I'm just a little confused as to how I would set up my equation.

Using Post #4 diagram:

Σx = -O_x-C_x-A_x-D_x

and Σx = Σy = Σz

and radius for O_x, C_x, A_x, D_x = s = 0.148 m

Is this right?

 

[PeroK]

Hi, I'm just a little confused as to how I would set up my equation.

Using Post #4 diagram:

Σx = -O_x-C_x-A_x-D_x

and Σx = Σy = Σz

and radius for O_x, C_x, A_x, D_x = s = 0.148 m

Is this right?

I don't follow that. For any charge, there are only four charges for which the force has an x-component. One is a distance $s$ away; two are a distance $\sqrt 2 s$ away and one is a distance $\sqrt 3 s$ away.

 

[Steve4Physics]

Hi, I'm just a little confused as to how I would set up my equation.

Using Post #4 diagram:

Σx = -O_x-C_x-A_x-D_x

and Σx = Σy = Σz

and radius for O_x, C_x, A_x, D_x = s = 0.148 m

Is this right?

I don't understand what you are saying. It’s worth taking a few steps back.

So, we are using the Post #4 diagram (not the Post #1 diagram). Point K is (s, s, s) and we want the force on the charge at K (not the force on the charge at A).

Try this exercise.

Consider only 2 charges, the one at K (s, s, s) and the one at D (0, s, 0). Ignore the other charges.

Here are some questions for you.

In terms of k, q, s and any other values needed:
Q1. What is the distance between K and D?
Q2. What is the magnitude of the force acting on the charge at K due to the charge at D?
Q3. What is the x-component of this force?
Q4. What is the y-component of this force?
Q5. What is the z-component of this force?

If you can post your answers it will help us check your understanding.

 

[cherry]

I don't understand what you are saying. It’s worth taking a few steps back.

So, we are using the Post #4 diagram (not the Post #1 diagram). Point K is (s, s, s) and we want the force on the charge at K (not the force on the charge at A).

Try this exercise.

Consider only 2 charges, the one at K (s, s, s) and the one at D (0, s, 0). Ignore the other charges.

Here are some questions for you.

In terms of k, q, s and any other values needed:
Q1. What is the distance between K and D?
Q2. What is the magnitude of the force acting on the charge at K due to the charge at D?
Q3. What is the x-component of this force?
Q4. What is the y-component of this force?
Q5. What is the z-component of this force?

If you can post your answers it will help us check your understanding.

I tried using trig this time, I hope this is correct.

 

[Steve4Physics]

I tried using trig this time, I hope this is correct.
View attachment 338710

Looking good but some issues:

General: since you are using symbols for physical quantities, there is no need to put the units. You only need units when numerical values (for k, s and q) are entered. (Some poeple only put units on the final answer, but some people include units with all numerical values - it varies between establishments.)

3) and 5) Why have you used negative signs? The charges have the same sign so there is repulsion between them. If the charge at K is released, in what direction would it move (due to the force from charge D alone)?

Also, I’d be tempted to replace sin(45º) and (cos45º) by $\frac 1{\sqrt 2}$.

4) Yes.
_______________

To get the total force on K (the long way) you would need to:

i) find the x, y and z components of every force on K (there are 7 such forces; you've just worked out the components for one of them);

ii) Add all the x components to give the total X; add all the y components to give the total Y; add all the z components to give the total Z;

iii) Add (vector addition)) X, Y and Z to get the resultant force on K.

But there are shorts cuts which have been suggested in earlier posts.

 

[cherry]

Looking good but some issues:

General: since you are using symbols for physical quantities, there is no need to put the units. You only need units when numerical values (for k, s and q) are entered. (Some poeple only put units on the final answer, but some people include units with all numerical values - it varies between establishments.)

3) and 5) Why have you used negative signs? The charges have the same sign so there is repulsion between them. If the charge at K is released, in what direction would it move (due to the force from charge D alone)?

Also, I’d be tempted to replace sin(45º) and (cos45º) by $\frac 1{\sqrt 2}$.

4) Yes.
_______________

To get the total force on K (the long way) you would need to:

i) find the x, y and z components of every force on K (there are 7 such forces; you've just worked out the components for one of them);

ii) Add all the x components to give the total X; add all the y components to give the total Y; add all the z components to give the total Z;

iii) Add (vector addition)) X, Y and Z to get the resultant force on K.

But there are shorts cuts which have been suggested in earlier posts.

Hello again,

I'm still struggling to get the right answer. (used post #4 notation)

I think the part I messed up in was finding F_x, F_y, F_z of KO.
I calculated the angle using arccos(sqrt(2)s/sqrt(3)s). I then applied cos(theta) to all components of F of KO.
This is the part I am unsure about and am having trouble visualizing.

 

[PeroK]

Hello again,

I'm still struggling to get the right answer. (used post #4 notation)
View attachment 338713

I think the part I messed up in was finding F_x, F_y, F_z of KO.
I calculated the angle using arccos(sqrt(2)s/sqrt(3)s). I then applied cos(theta) to all components of F of KO.
This is the part I am unsure about and am having trouble visualizing.

The only problem is what you did with $\theta$. The distance from O to K is $\sqrt{s^2 + s^2 + s^2} = \sqrt 3 s$. So, the magnitude of this force must be $F_{OK} = \frac{kq^2}{3s^2}$

Now, by symmetry, the force of charge O on charge K must have the same component in every direction. Hence: $F_{OK}^2 = F_x^2 + F_y^2 + F_z^2 = 3F_x^2$.

And, finally, $F_x = F_y = F_z = \frac 1 {\sqrt 3}F_{OK}$. I think that's all you're missing.

PS note that in general if you want the angle of a vector with an axis, then you can take the scalar (dot) product. In general, for the x-axis:
$$v_x = \vec v \cdot \vec i = |\vec v|\cos \theta_x$$$$\Rightarrow \ \cos \theta_x = \frac{v_x}{|\vec v|} = \frac{v_x}{\sqrt{v_x^2 + v_y^2 + v_z^2}}$$So, in your case, the $\theta$ you were trying to calculate satisfied $\cos \theta = \frac 1 {\sqrt 3}$.

 

[cherry]

The only problem is what you did with $\theta$. The distance from O to K is $\sqrt{s^2 + s^2 + s^2} = \sqrt 3 s$. So, the magnitude of this force must be $F_{OK} = \frac{kq^2}{3s^2}$

Now, by symmetry, the force of charge O on charge K must have the same component in every direction. Hence: $F_{OK}^2 = F_x^2 + F_y^2 + F_z^2 = 3F_x^2$.

And, finally, $F_x = F_y = F_z = \frac 1 {\sqrt 3}F_{OK}$. I think that's all you're missing.

PS note that in general if you want the angle of a vector with an axis, then you can take the scalar (dot) product. In general, for the x-axis:
$$v_x = \vec v \cdot \vec i = |\vec v|\cos \theta_x$$$$\Rightarrow \ \cos \theta_x = \frac{v_x}{|\vec v|} = \frac{v_x}{\sqrt{v_x^2 + v_y^2 + v_z^2}}$$So, in your case, the $\theta$ you were trying to calculate satisfied $\cos \theta = \frac 1 {\sqrt 3}$.

I got it - thank you so much!