Eccentric anomaly of ellipse-circle intersections

[Marko7]

I want to calculate eccentric anomaly of all points of ellipse-circle intersection.
Ellipse is not rotated and its center is in origin.
Circle can be translated to (Cx, Cy) coordinates.
I am using python for calculations.

Only solution I found, is this:
https://math.stackexchange.com/questions/3419984/find-the-intersection-of-a-circle-and-an-ellipse
And I implemented it in my code. I avoided calculating polynomial roots manually by using numpy's solver.

[CODE lang="python" title="ellipse_circle.py"]import numpy as np

def ellipse_circle(a, b, c_x, c_y, r):
"""Calculate eccentric anomalies of intersecting points
on non-rotated ellipse in origin, and translated circle"""

# quartic equation coefficients
a_4 = a**2 * (c_y**2 - b**2) + b**2 * (c_x - r)**2
a_3 = 4 * a**2 * r * c_y
a_2 = 2 * (a**2 * (c_y**2 - b**2 + 2*r**2) + b**2 * (c_x**2 - r**2))
a_1 = 4 * a**2 * r * c_y
a_0 = a**2 * (c_y**2 - b**2) + b**2 * (c_x + r)**2

# quartic equation roots
roots = np.polynomial.polynomial.polyroots([a_0, a_1, a_2, a_3, a_4])

# take only non-complex roots
real_roots = np.real(roots[np.isreal(roots)])

return real_roots % (2*np.pi)[/CODE]

I tested it on some simple example:
>>> ellipse_circle(5, 2.17945, 4.5, 0, 1)
array([5.22599703, 1.05718828])

But those two roots are not eccentric anomalies of intersection points, as can be seen here (Point D is real intersection, and point A is calculated one):

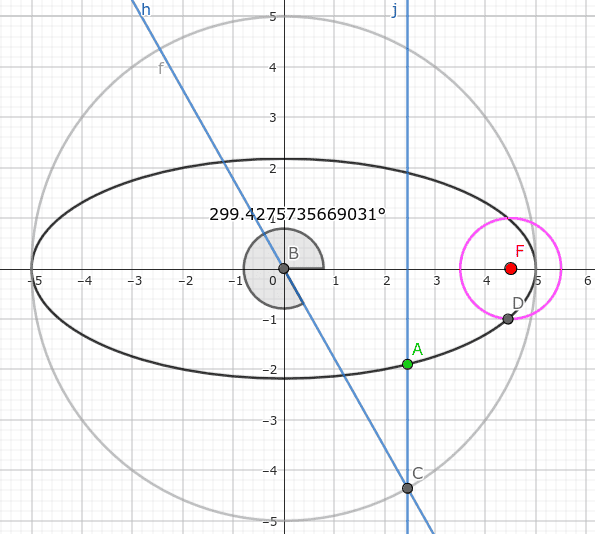
So, what am I doing wrong, how can I calculate eccentric anomaly?

 

[pasmith]

You are calculating values for the parameter $z \in \mathbb{R}$ in the parametrization of the circle $(x-x_c)^2 + (y-y_c)^2 = r^2$ as
$$\begin{split}<br /> x = x_c + r \frac{1 - z^2}{1 + z^2} \\<br /> y = y_c + r \frac{2z}{1 + z^2}. \end{split}$$ $z$ is not an angle, so I do not think it is necessary or correct to return these modulo $2\pi$, as your program does (see line 20). Replace line 20 with

   return real_roots

and see if it does any better.

EDIT: Note that the point $(x_c - R, y_c)$ is attained only in the limit $|z| \to \infty$; this corresponds to the coefficient of $z^4$ vanishing. You can test this case by setting cx = -0.5, cy = 0, r = 0.5, a = b = 1.

I also now see from your diagram that you have misinterpreted the root 5.22 as being an angle in radians about the origin (5.22 rad ~ 299 deg); it is not. You need to use the above parametrization of the circle to recover the x and y coordinates. The eccentric anomaly can then be calculated as $$\arccos\left(\frac{1}{\sqrt{1 - b^2/a^2}}\left(1 - \frac{\sqrt{(x-ae)^2 + y^2}}{a}\right)\right)$$ as shown here.

 

[Marko7]

I had no idea that parameter is from circle.
I thought that parameter $z$ is same as parameter $t$ as used in normal parametric equations.

Here is working code if anyone in future needs it:
[CODE lang="python" title="ellipse_circle.py"]
import numpy as np
def ellipse_circle(a, b, c_x, c_y, r):
"""Calculate eccentric anomalies of intersecting points
on non-rotated ellipse in origin, and translated circle"""
# quartic equation coefficients
a_0 = a**2 * (c_y**2 - b**2) + b**2 * (c_x + r)**2
a_1 = 4 * a**2 * r * c_y
a_2 = 2 * (a**2 * (c_y**2 - b**2 + 2*r**2) + b**2 * (c_x**2 - r**2))
a_3 = 4 * a**2 * r * c_y
a_4 = a**2 * (c_y**2 - b**2) + b**2 * (c_x - r)**2

# quartic equation roots
roots = np.polynomial.polynomial.polyroots([a_0, a_1, a_2, a_3, a_4])
# take only non-complex roots
real_roots = np.real(roots[np.isreal(roots)])

if any(real_roots):
# calculate x and y coordinates
x = c_x + r * (1-real_roots**2) / (1 + real_roots**2)
y = c_y + r * 2 * real_roots / (1 + real_roots**2)
ecc = np.sqrt(1-(b**2/a**2))
# eccentric anomaly
ea = np.arccos((1/np.sqrt(1-(b**2)/a**2)) * (1-(np.sqrt((x-a*ecc)**2 + y**2)/a)))
ea = np.where(real_roots < 0, 2*np.pi-ea, ea) # quadrant corrections
return ea
else:
return np.array([])
[/CODE]
Note: because of square roots in line 23, calculated angle is in range (0, $\pi$), which is corrected in line 24.
Resulting eccentric anomaly is in range (0, $2\pi$).

In my simulation it is very unlikely that this edge case with $z^4$ coefficient being zero will occur, so I just omitted it to save computation time.

Thanks. Helped a lot!

 

[pasmith]

Thinking again, it is simpler to obtain the anomaly from $(x,y)$ as

np.arctan2(np.sign(y)*np.sqrt(a**2 - x**2),x)

since the auxiliary circle of the ellipse is $x^2 + y^2 = a^2$.

EDIT: Simpler still is

atan2((a/b)*y, x)

since $(x,y) \mapsto (x,(a/b)y)$ maps the ellipse $(a\cos\theta, b\sin \theta)$ to the circle $(a \cos \theta, a \sin \theta)$.

 

[pasmith]

A further refinement is to parametrize the ellipse, rather than the circle, as $$\begin{split}<br /> x &= a\frac{1 - z^2}{1 + z^2} \\<br /> y &= b\frac{2z}{1 + z^2} \end{split}$$ and then the values of $z$ at the points of intersection are the roots of $P(z) = \sum_{n=0}^4 a_nz^n = 0$ where $$\begin{split}<br /> a_0 &= a^{2} - 2 a c_{x} + c_{x}^{2} + c_{y}^{2} - r^{2} \\<br /> a_1 &= - 4 b c_{y} \\<br /> a_2 &= - 2 a^{2} + 4 b^{2} + 2 c_{x}^{2} + 2 c_{y}^{2} - 2 r^{2} \\<br /> a_3 &= - 4 b c_{y} \\<br /> a_4 &= a^{2} + 2 a c_{x} + c_{x}^{2} + c_{y}^{2} - r^{2}<br /> \end{split}$$ The anomalies are then obtained by

[
    np.atan2(2*z, 1.0 - z**2 ) for z in roots if np.isreal(z)
]

with the addition of $\pi$ if the degree of $P$ is less than 4.