Efficiency of a cycle from a diagram

[fluidistic]

Homework Statement

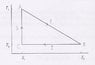
Calculate the efficiency of the heat machine that is shown in the figure. Draw the corresponding Carnot cycle diagram in the S-T plane.

Homework Equations

\varepsilon = \frac{ \Delta W}{\Delta Q}.
\Delta Q = T \Delta S

The Attempt at a Solution

My problem lies in evaluating \Delta Q for the process 1 (or from A to B).
For the process 2, \Delta Q=T_2(S_2-S_1).
For the process 3, \Delta Q=0 because there's no change in entropy.
But I'm stuck at process 1. My attempt was \Delta Q=\Delta T \Delta S=(T_2-T_1)(S_2-S_1) but I know this doesn't make any sense.
Using that non sensical result I find \varepsilon = \frac{1}{T_2-\frac{T_2^2}{T_1}} which makes no sense because if T_1=T_2 I get an infinite efficiency while I should get 0. A friend of mine reached \varepsilon =\frac{T_1-T_2}{T_1+T_2} but I don't know how he did nor if that's right either.
Any help is appreciated.

 

[I like Serena]

Did you consider that $dQ=TdS$, and that if T changes with S that then $ΔQ=∫TdS$?

 

[fluidistic]

Did you consider that $dQ=TdS$, and that if T changes with S that then $ΔQ=∫TdS$?

Actually not! haha.
Now I reach the same answer as my friend. Thank you very much for that.
Hmm I'll think about the Carnot cycle. If I need help I'll post here.