kent davidge
- 931
- 56
(sorry for my poor english) I've read that a electromagnetic wave only exists in a particular point of space if in such a point there is a nonlinear change of the electric field in respect to time. Then I took a graph calculator and I derived Coulombs equation for the electric field. The results are shown below.
What surprised me was that when the charge is accelerating, the curve of the rate of change of the field in two points on the same horizontal axis has different forms (maximum points are different). Has it anything to do with the statement I mentioned above? Also, even so I don't know why would it be a wave if these two points has different rate of change at the same time.
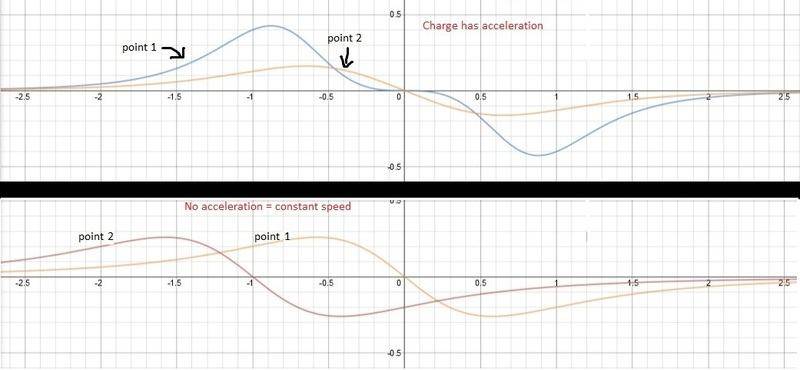
What surprised me was that when the charge is accelerating, the curve of the rate of change of the field in two points on the same horizontal axis has different forms (maximum points are different). Has it anything to do with the statement I mentioned above? Also, even so I don't know why would it be a wave if these two points has different rate of change at the same time.
Last edited: