Yalanhar
- 39
- 2
- Homework Statement
- uniformly charged disk, radius r, with surface charge density ##\sigma##
. I want to find the electric field along the axis through the centre of the disk at a h distance
- Relevant Equations
- ##dE=\frac {kdq}{r^2}##
Homework Statement: uniformly charged disk, radius r, with surface charge density ##\sigma##
. I want to find the electric field along the axis through the centre of the disk at a h distance
Homework Equations: ##dE=\frac {kdq}{r^2}##
My Solution:
##dE=\frac {kdq}{r^2}##
in this case r=s
##dE=\frac {kdq}{s^2}##
##dq=\sigma dA## where: ##dA=2\pi rdr##
##dq={\sigma 2\pi rdr }##
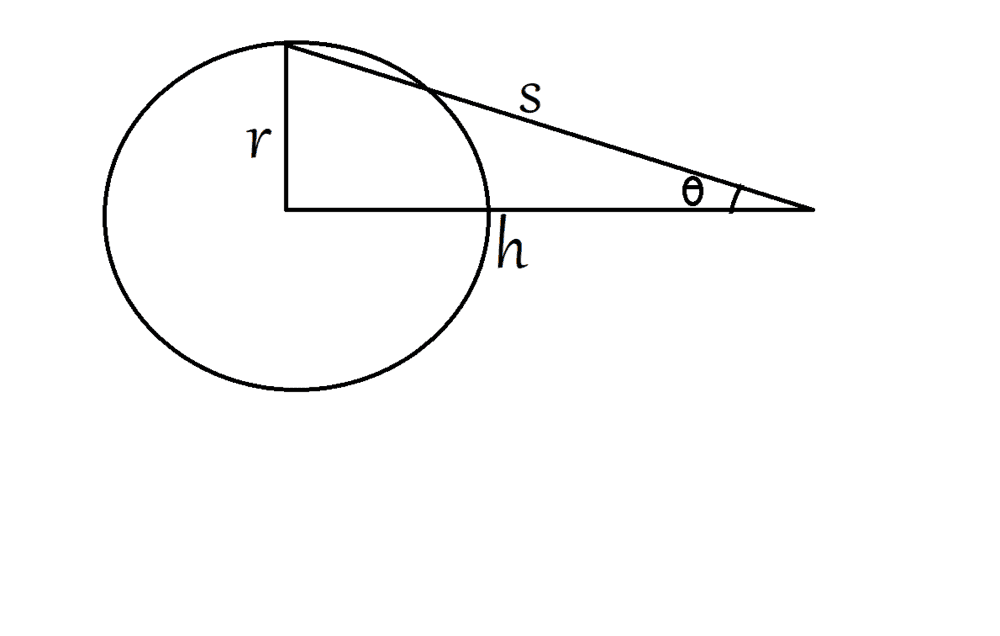
##dE=\frac {1}{4\pi \epsilon_{o}}\frac {2\sigma \pi rdr}{s^2}cos\theta##
##dE=\frac {1}{2 \epsilon_{o}}\frac {\sigma rdr}{s^2}cos\theta## (1)
in the triangle:
##tan\theta = \frac {r}{h}## therefore : ##r = htan\theta## (2) and ##dr=\frac{hd\theta}{cos^2\theta}##(3)
##cos\theta = \frac {h}{s}## therefore : ##s = \frac {h}{cos\theta}##(4)
(2),(3) and (4) in (1)
##dE=\frac {1}{2 \epsilon_{o}}\frac {\sigma htan\theta (\frac{hd\theta }{cos^2\theta}) cos\theta }{(\frac {h}{cos\theta})^2}##
##dE=\frac{\sigma sin\theta d\theta}{2\epsilon_{0}}##
##E=\frac {\sigma}{2\epsilon_{o}}\int_0^\theta sin\theta \,d\theta##
So:
##E=\frac{\sigma}{2\epsilon_{o}}(1-cos\theta)##
Using ##cos\theta=\frac{h}{\sqrt {r^2 + h^2}}##
##E=\frac{\sigma}{2\epsilon_{o}}(1-\frac{h}{\sqrt{ r^2 + h^2}})##
Is it correct? Normally students don't do this way, so I am not sure. Also, why in the integration I don't need to multiply by 2? ##\theta## isn't only for the first half?
. I want to find the electric field along the axis through the centre of the disk at a h distance
Homework Equations: ##dE=\frac {kdq}{r^2}##
My Solution:
##dE=\frac {kdq}{r^2}##
in this case r=s
##dE=\frac {kdq}{s^2}##
##dq=\sigma dA## where: ##dA=2\pi rdr##
##dq={\sigma 2\pi rdr }##
##dE=\frac {1}{4\pi \epsilon_{o}}\frac {2\sigma \pi rdr}{s^2}cos\theta##
##dE=\frac {1}{2 \epsilon_{o}}\frac {\sigma rdr}{s^2}cos\theta## (1)
in the triangle:
##tan\theta = \frac {r}{h}## therefore : ##r = htan\theta## (2) and ##dr=\frac{hd\theta}{cos^2\theta}##(3)
##cos\theta = \frac {h}{s}## therefore : ##s = \frac {h}{cos\theta}##(4)
(2),(3) and (4) in (1)
##dE=\frac {1}{2 \epsilon_{o}}\frac {\sigma htan\theta (\frac{hd\theta }{cos^2\theta}) cos\theta }{(\frac {h}{cos\theta})^2}##
##dE=\frac{\sigma sin\theta d\theta}{2\epsilon_{0}}##
##E=\frac {\sigma}{2\epsilon_{o}}\int_0^\theta sin\theta \,d\theta##
So:
##E=\frac{\sigma}{2\epsilon_{o}}(1-cos\theta)##
Using ##cos\theta=\frac{h}{\sqrt {r^2 + h^2}}##
##E=\frac{\sigma}{2\epsilon_{o}}(1-\frac{h}{\sqrt{ r^2 + h^2}})##
Is it correct? Normally students don't do this way, so I am not sure. Also, why in the integration I don't need to multiply by 2? ##\theta## isn't only for the first half?
Last edited: