Electric field due to a spherical charged shell (direct integration)

[schrodingerscat11]

Homework Statement

Find the electric field a distance z from the center of a spherical surface of radius R which carries a uniform density σ. Treat the case z<R (inside) as well as z>R (outside). Express the answers in terms of the total charge q on the sphere.

Homework Equations

$E = \int \frac{dq~\hat({r-r'})}{(r-r')^2}$
where r is the vector from origin to the point where electric field will be evaluated and
r' is the vector from origin to the location of dq (source of electric field)

Let $r-r' = ζ$

The Attempt at a Solution

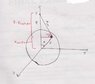
(Attached is the sketch of the figure for reference.)

We treat it as a hollow thin shell and divide it in into infinitesimal dA. In spherical coordinates,
$dA = R^2~sinθ~dθdψ$
$dq = σdA$
$dA =σ R^2~sinθ~dθdψ$

Also, the ζ vector is just
$ζ^2=z^2+R^2 - 2Rz cosθ$ via cosine law

Clearly, the total electric field felt at point p (a distance z) above the sphere is just in the z direction since the other components cancel. Therefore, we can just get the z component of E-field due to charge dq and add all of them together for the entire sphere.

$dE_{z} = dE \hat{z}$
$dE_{z} = dE sin ω$
$dE_{z} = dE \frac {z-Rcosθ}{ζ}$

Electric field therefore is
$E = \int \frac{dq~\hat{ζ}}{ζ^2}$
$E = \frac{1}{4πε_o}\int\frac{σR^2~sinθdθdψ}{z^2+R^2-2Rzcosθ}\frac{z-Rcosθ}{\sqrt{z^2+R^2-2Rzcosθ}}$

since $\int_0^{2π} = ψ~dψ = 2π$
and if we let u = Rcos du = -Rsinθ dθ
and noting that u=1 when θ=0 and u=-1 when θ=π

$E = \frac{2πσR^2}{4πε_oR}~\int_{-1}^{1}\frac{(z-u)du}{(z^2+R^2-2zu)^\frac{3}{2}}$

Now, how do I integrate this? Any ideas? Thanks a lot.

 

[Saitama]

Nice work so far!

The final integral is:
$$2k\pi\sigma R^2\int_0^{\pi} \frac{z-R\cos\theta}{(z^2+R^2-2Rz\cos\theta)^{3/2}}\sin\theta\,d\theta=2k\pi \sigma \int_0^{\pi} \frac{a-\cos\theta}{(a^2-2a\cos\theta+1)^{3/2}}\sin\theta\,d\theta$$
where $a=\dfrac{z}{R}$.

Next, use the substitution $a^2-2a\cos\theta+1=t^2 \Rightarrow \sin\theta\,d\theta=\dfrac{t\,dt}{2a}$. Can you simplify the integral now? Notice that the new limits for integral are perfect squares!

 

[schrodingerscat11]

Hmm.. That was simpler.. Thank you very much! I think I can take it from here.. Also, sorry for the very late reply.. I had a very busy week. Many thanks again! :)

 

[Saitama]

Hmm.. That was simpler.. Thank you very much! I think I can take it from here.. Also, sorry for the very late reply.. I had a very busy week. Many thanks again! :)

Glad to help!

 

[Vishesh Sharma]

I have a doubt in the very starting we should have found the magnitude of (r-r') and then square it. So, in this case why it is not (r2+z2 ) because of its magnitude first and then square. Please Explain

 

[TSny]

I have a doubt in the very starting we should have found the magnitude of (r-r') and then square it. So, in this case why it is not (r2+z2 ) because of its magnitude first and then square. Please Explain

Can you explain why you believe that $|\vec{r} - \vec{r}'|^2$ is equal to $r^2 + z^2$? If would be helpful if you could show a diagram with $\vec{r}$, $\vec{r}'$, and $z$ labeled.

 

[Vishesh Sharma]

I got my mistake I was taking angle between r and z to be 90. Thank you for pointing out the mistake,and also the integration method was really good.
Thanks again.

 

[Vishesh Sharma]

Am I missing something? Why not just go with Gauss's theorem?

Its probably because that relevant equations work for every surface, although gauss law is also applicable to any surface but we can find out easily only for symmetrical surfaces. This was just for practice. I believe gauss law is much better technique in this question.