How is the Electric Field in Energy Bands Calculated?

[jisbon]

Homework Statement

The energy band in a semiconductor sample is given by
$6.67x^2$
eV, where x is the distance and is valid from 0 to 3m.
(i)Sketch energy band diagram, indicating valence and conduction bands, energy gap and direction of x.
(ii)Determine the electric field in terms of V and m as a function of distance x and indicate the direction of the electric field in the energy band diagram.
(iii)Calculate the electric field at x=3m (in terms of and m)

Relevant Equations

-

This is my attempt at this question, and I'm probably wrong, will need some help/guidance from the experts here :/

i)

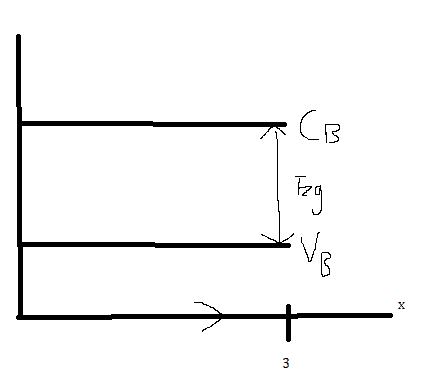
(ii)

Since energy band given by $6.67x^2$, can I assume that electric field is simply the energy difference from 0-3m divided by 3m? In this case, would the answer simply be (6.67*3*3)-(6.67*0*0)/3= 20.01V/m?

(iii)At x=3, will the electric field be simply 20.01*3=60.03?

Cheers

 

[trurle]

(iii)At x=3, will the electric field be simply 20.01*3=60.03?

Cheers

No. To get field, you need to take derivative of potential, not simply divide by distance. After taking derivative, the answer is E(x)=2*x*6.67