- #1
CMLeo
- 2
- 1
Homework Statement
Hello everyone,
I am writing here regarding a doubt I have about electric fields. Our set up consists on two rod shape electrodes in a cylindrical glass vessel separated by 6 mm from each other, with one of the electrodes grounded (electrodes dimensions: 0.5 mm diameter and 10 cm long). As far as I know the electric field between the electrodes is constant for uniform DC fields, but we have here an inhomogeneous field and I am not quite sure how to calculate the electric field gradient. A voltage up to 400 V is supplied within the system (dielectric solvent, so no current is induced and no chemical reaction is expected).
Homework Equations
Calculate the electric field and voltage in 1, 2, and 3 as a function of the distance.
The Attempt at a Solution
[/B]
The voltage and electric field of a charge cylinder as a function of the distance is given by:
E(r)= λ/(2πεr) r≥a
V(r)= (λ ln(a/r))/(2πε) r≥a
where λ is the charge per unit length, ε is the permittivity of the free space, a is the radius of the cylinder, and R is the distance from one of the electrodes. V=400 V at the charged electrode and 0 V at the grounded electrode.
First, I think I should replace the permittivity of the free space for the medium (ε'=ε x εm). For a point co-linear with the centres of each cylinder we have an electric field in 2 equal to:
At 1:
At 3:
For the potential difference between the electrodes:
At 2:
At 1 and 3, respectively:
I am not sure whether this attempt is right or not. Besides, I would like to have the electric field without the charge per unit length since I do not know how to calculate with the information I have. So, I thought in obtain λ as a function of the voltage (I have the supply voltage) and replace it in the E equation. However, I do not know if this would work since the voltage at the second electrode is 0 V, should I assume that beyond the second electrode I have 0 V and the walls of the vial are 0 V as well?
Thanks in advance for any help.
Attachments
-
 upload_2018-1-15_9-29-15.png12 KB · Views: 658
upload_2018-1-15_9-29-15.png12 KB · Views: 658 -
 upload_2018-1-15_9-53-25.png11.7 KB · Views: 1,982
upload_2018-1-15_9-53-25.png11.7 KB · Views: 1,982 -
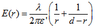 upload_2018-1-15_9-55-33.png892 bytes · Views: 574
upload_2018-1-15_9-55-33.png892 bytes · Views: 574 -
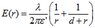 upload_2018-1-15_9-59-14.png890 bytes · Views: 601
upload_2018-1-15_9-59-14.png890 bytes · Views: 601 -
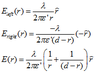 upload_2018-1-15_10-16-40.png1.7 KB · Views: 1,030
upload_2018-1-15_10-16-40.png1.7 KB · Views: 1,030 -
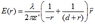 upload_2018-1-15_10-17-41.png981 bytes · Views: 960
upload_2018-1-15_10-17-41.png981 bytes · Views: 960 -
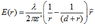 upload_2018-1-15_10-19-30.png984 bytes · Views: 944
upload_2018-1-15_10-19-30.png984 bytes · Views: 944 -
 upload_2018-1-15_10-48-24.png2 KB · Views: 986
upload_2018-1-15_10-48-24.png2 KB · Views: 986 -
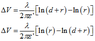 upload_2018-1-15_10-53-5.png1.1 KB · Views: 956
upload_2018-1-15_10-53-5.png1.1 KB · Views: 956