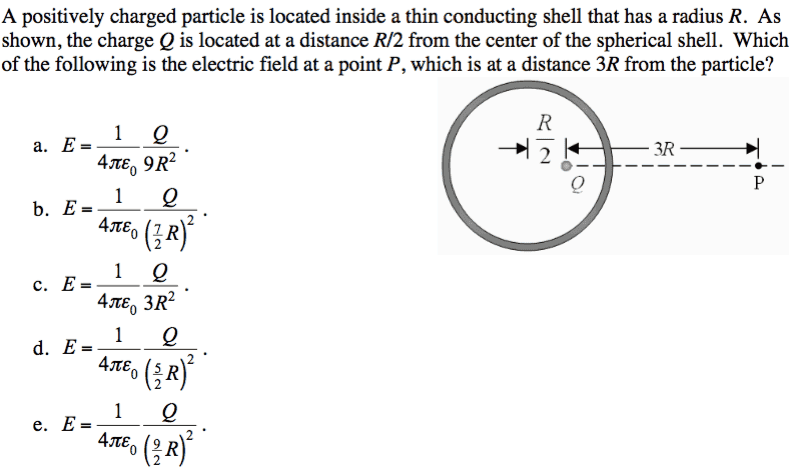The discussion centers on calculating the electric field near a conducting shell with an internal charge. Participants emphasize the importance of Gauss's Law in determining the electric field and potential around the shell. The charge induces a corresponding charge on the inner surface of the shell, leading to a uniform potential across the shell's surface. The discussion highlights the necessity of understanding symmetry in electrostatic configurations to apply these principles effectively.
PREREQUISITESStudents of physics, electrical engineers, and anyone interested in understanding electrostatics and the behavior of electric fields around conductors.
Induces a charge in the inner surface of the shell?PeroK said:
Have you studied that? Or, learned any techniques to find the electric field outside an asymmetric charge configuration?lys04 said:
I've learnt Gauss's law, if that's applicable.PeroK said:
Gauss's law is useful. What can you say about the potential on the surface of a conductor?lys04 said:
In a way: you will have to argue why the required symmetry (*) is present.lys04 said:
It's uniform?PeroK said:
Yeah I'm not sure about thatBvU said:
Yes. The surface of the shell must be an equipotential. Now, the potential is fully determined by the boundary conditions (technically this is a uniqueness property of electrostatic solutions). You know that outside the shell a spherically symmetric potential is a solution, so it must be the only solution.lys04 said: