Electric field needed to tear a conducting sphere

[ermia]

Homework Statement

This is one of krotov problems. The image is uploaded below.
The whole thing is easy but why force per unit length is equal in both cases while the thicknesses are equal?

Relevant Equations

nothing special

..

 

[kuruman]

This is also a homework problem in Physics Forums that requires you to show some effort towards a solution. Please show us your solution and tell us what's troubling you about it. Also, "nothing special" is not relevant and it's not even an equation.

 

[hutchphd]

The strength of any glue joint is proportional to the contact area of the glue. So if the hemisphere shells of thickness t and radius r are glued together the rending force required will be proportional to $$ F_{rend}~ \alpha~rt $$
Knowing this please show us your solution to the problem

 

[ermia]

The strength of any glue joint is proportional to the contact area of the glue

Why?
And why this happens to electric field

So if the hemisphere shells of thickness t and radius r are glued together the rending force required will be proportional to Frend α rt

Why? t is not a differential to say $$A=2\pi r t$$
b.t.w: I don't have doubt about whole question. Just the part I asked.
I thought the answer of my question was sth obvious cause all solutions in the internet or the book refused explaining it but I couldn't understand why this happend?

 

[haruspex]

Why?

I would have thought that obvious. If a joint area A can take force F, then a second joint area A in parallel can take F. Between them they can withstand a force 2F.

And why this happens to electric field

It has nothing to do with what the source of the force is.

Why? t is not a differential to say $$A=2\pi r t$$
b.t.w: I don't have doubt about whole question. Just the part I asked.

t is the a thickness, which we are told is small, so the area of the annulus is approximately $2\pi r t$.

 

[ermia]

I would have thought that obvious. If a joint area A can take force F, then a second joint area A in parallel can take F. Between them they can withstand a force 2F.

Why the pressures for two different spheres at the area middle of themselves should be equal to each other??

 

[Orodruin]

will be proportional to $$ F_{rend}~ \alpha~rt $$

The LaTeX you are looking for is \propto:
$$
F_{\rm rend} \propto rt
$$

 

[haruspex]

Why the pressures for two different spheres at the area middle of themselves should be equal to each other??

Since you have not posted the solution I struggle to understand what you are asking.
Please post the solution, indicating exactly which step is the problem.

 

[ermia]

Since you have not posted the solution I struggle to understand what you are asking.
Please post the solution, indicating exactly which step is the problem.

I uploaded it here.

It has nothing special for me except the part I asked.
Since the thickness of the sphere walls remains unchanged, the force tearing the sphere per unit length must remain unchange
but why?

 

[vela]

It has nothing special for me except the part I asked.
Since the thickness of the sphere walls remains unchanged, the force tearing the sphere per unit length must remain unchange
but why?

It seems obvious why it wouldn't change. Why do you think it would change?

 

[Lnewqban]

I uploaded it here.

It has nothing special for me except the part I asked.
Since the thickness of the sphere walls remains unchanged, the force tearing the sphere per unit length must remain unchange
but why?

Because that is the maximum stress that the material of that sphere allows before failing.
More perimetral area requires stronger pulling force to separate the sphere.

Please, see:
https://en.wikipedia.org/wiki/Stress_(mechanics)#Simple_stress

https://en.wikipedia.org/wiki/Ultimate_tensile_strength

 

[TSny]

Why the pressures for two different spheres at the area middle of themselves should be equal to each other??

As others have stated, it will take twice as much force to break apart twice as much joined area. That is, the force F required to separate a given area A is proportional to the area. Thus, there is a proportionality constant c such that F = cA. But pressure P is defined as force per unit area: P = F/A.

So, P = (cA)/A = c = a constant independent of the area.

The value of the constant c depends on the properties of the material. Since the two spheres that you are considering are made of the same material, c is the same for the two spheres. So the required pressure is the same for the two spheres.

In your original post, you asked

The whole thing is easy but why force per unit length is equal in both cases while the thicknesses are equal?

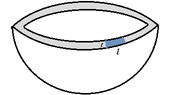
For a patch length $l$ and thickness $t$ as shown, the area of the patch is $A = lt$.

So, the force required to disjoin this area is $F = cA = clt$. Thus, the force per unit length is $F/l = clt/l = ct$. Since $c$ and $t$ are the same for the two spheres, the force per unit length required to split the sphere is the same for the two spheres.