power freak
- 6
- 0
Hi,
I'm in the process of completing my physics coursework (A-level) and have run into a bit of a problem:
I am trying to find a general equation for a plate capacitor, where the plates aren't parallel.
I've always seen the parallel plate capacitor equation:
C = \frac {\epsilon A}{d}
Derived through finding an expression for the electric field due to parallel plates and substituting this into:
C = \frac {Q}{V}
I was intending to use a similar approach to the problem with non-parallel plates (perhaps there is a better way?)
This runs into a problem however because I do not know how to derive an expression for the electric field between non-parallel plates. Could somebody please point me in the right direction?
An attempt at deriving an expression:
The electric field due to sheet of charge is:
E = \frac {\sigma}{2\epsilon}
If the normal to the plate makes an angle \theta to the field lines then the electric field is:
E = \frac {\sigma Cos(\theta)}{2\epsilon}
So the field between angled plates would be:
E = \frac {\sigma(1 + Cos(\theta))}{2\epsilon}
(sigmas represent charge density, thetas represent the angle to the normal and epsilons represent the permittivity of the dielectric.)
However if I then use this to derive an equation for the capacitance C then it doesn't match my experimental data at all (in some places it is out by nearly 100% where as the accuracy of my measuring equipment was roughly 3%.)
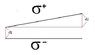
I've attached a quick diagram too, just to give an idea of what is going on (I know my english isn't as clear as it could be.) The black lines are the plates, the dark red lines are just there to give distances etc. The lower case sigmas represent the charge density of each plate.
Any help would be much appreciated,
Lewis
EDIT: actually thinking about it.. To do the "substitution" method I'm going to need to multiply the electric field by a distance separation (d).. As the distance isn't linear this isn't going to work... Back to the drawing board again I guess?
I'm in the process of completing my physics coursework (A-level) and have run into a bit of a problem:
I am trying to find a general equation for a plate capacitor, where the plates aren't parallel.
I've always seen the parallel plate capacitor equation:
C = \frac {\epsilon A}{d}
Derived through finding an expression for the electric field due to parallel plates and substituting this into:
C = \frac {Q}{V}
I was intending to use a similar approach to the problem with non-parallel plates (perhaps there is a better way?)
This runs into a problem however because I do not know how to derive an expression for the electric field between non-parallel plates. Could somebody please point me in the right direction?
An attempt at deriving an expression:
The electric field due to sheet of charge is:
E = \frac {\sigma}{2\epsilon}
If the normal to the plate makes an angle \theta to the field lines then the electric field is:
E = \frac {\sigma Cos(\theta)}{2\epsilon}
So the field between angled plates would be:
E = \frac {\sigma(1 + Cos(\theta))}{2\epsilon}
(sigmas represent charge density, thetas represent the angle to the normal and epsilons represent the permittivity of the dielectric.)
However if I then use this to derive an equation for the capacitance C then it doesn't match my experimental data at all (in some places it is out by nearly 100% where as the accuracy of my measuring equipment was roughly 3%.)
I've attached a quick diagram too, just to give an idea of what is going on (I know my english isn't as clear as it could be.) The black lines are the plates, the dark red lines are just there to give distances etc. The lower case sigmas represent the charge density of each plate.
Any help would be much appreciated,
Lewis
EDIT: actually thinking about it.. To do the "substitution" method I'm going to need to multiply the electric field by a distance separation (d).. As the distance isn't linear this isn't going to work... Back to the drawing board again I guess?
Attachments
Last edited: