Electric Fields through dielectrics

[Samson4]

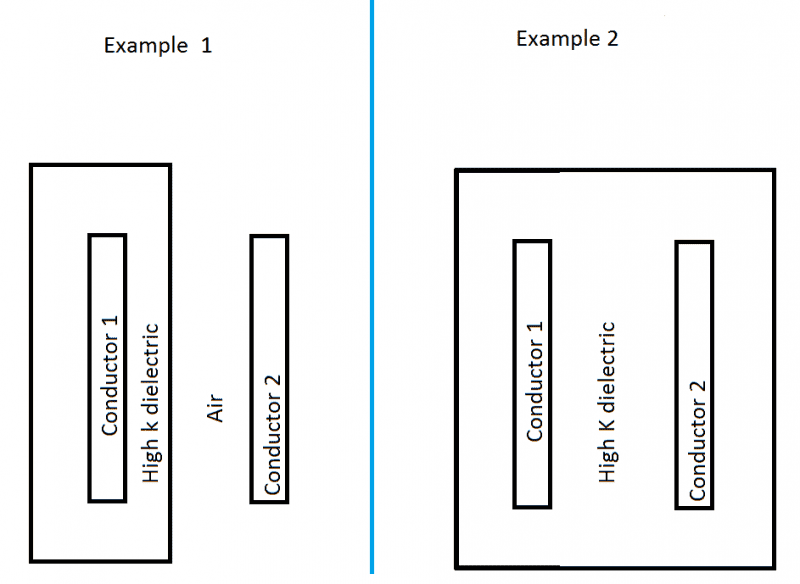
My question is simple; yet, I can not find the answer. In the picture below, all variables are identical; the plate separations, surface area, etc. The only difference is the fact that example 1 has 2 different dielectrics. Better yet, it has a dielectric that doesn't extend the entire distance between the two conductors.

1.Does example 1 and 2 have the same capacitance?

My understanding: conventional physics explains that the dielectric opposes the electric field. With that in mind, both should have the same capacitance.

2. Does that mean the dielectric is actually creating an electric field that permeates another dielectric? This being air in example 1.

3. If air has a dielectric strength slightly higher than vacuum, shouldn't it oppose the field from conductor 1 and the field from the high k dielectric? This would mean example 1 has a higher capacitance, correct?

 

[melthengylf]

the dielectric generates an opposing electric field. as a consecquence, electric field is lesser than with vacuum, which is the best dielectric. equivalently, the capacitance of a filledcapacitor is lesser than the one with vacuum. the word in spanish is "apantallar", i don't remember the word in english

 

[Samson4]

What?

If the electric field is "lesser", the capacitance is higher. I also think you are confusing dielectric strength and dielectric constant.

 

[melthengylf]

yes, i got confused, capacity is higher. and dielectric strength is irrelevant for low fields. what's relevant is dielectric constant. so, if dielectric constant of k is greater than the air, the capacitance of 2 will be greater.

 

[Samson4]

Both capacitors have a high k dielectric, why does capacitor 2 have a higher capacitance? Dielectric thickness is not apart of capacitance formulas, so is it not irrelevant? From my understanding, conductors and dielectrics react to electric fields in very 2 dimensional ways.

I still think they are equal or example 1 has higher capacitance. This is so confusing.

 

[nsaspook]

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/dielec.html

 

[Samson4]

See, no mention of thickness. Since the materials atomic structure defines it's dielectric constant, would that mean it doesn't have to expand the entire gap between the conductors?

 

[nsaspook]

See, no mention of thickness. Since the materials atomic structure defines it's dielectric constant, would that mean it doesn't have to expand the entire gap between the conductors?

Unless the air gap is at the same scale of the polar molecules gap the air dielectric will modify the physical capacitance of the circuit.

http://web.mit.edu/8.02t/www/materials/StudyGuide/guide05.pdf
Example 5.6 and
5.9.2 Capacitor with Dielectrics

 

[Samson4]

How does the electric field gain strength once it has left the polar molecules?

That would also mean the field the polar molecules are making are only internal, when they must be external by definition.

 

[melthengylf]

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/pplate.html
And then you use the equation for capacitor in series 1/Ct=1/C1+1/C2

 

[Samson4]

What are you talking about? How is that related?

 

[Svein]

In example 1 you have two capacitors in series, one with dielectric ε_K and one with dielectric ε₀. In example 2, you have just one capacitor, with dielectric ε_K. Do you need the formula for calculating the capacitance?

 

[Samson4]

There is one capacitor in example one. For there to be two I would need at least another conductor.

 

[Svein]

There is one capacitor in example one. For there to be two I would need at least another conductor.

No. You can calculate the capacitance between any two elements. I just used the border between the high k dielectric and air as one (virtual) plate.

If you want to, imagine a very thin plate at this border and let the thickness →0.

 

[melthengylf]

Its equivalent, it's a conductor of length zero

 

[Samson4]

Hell yes, now I see it. The effective distance of the plate separation changes. Thank you guys so much.