Electric potential at the vertex of a triangle

[math4everyone]

I am stuck with this problem:

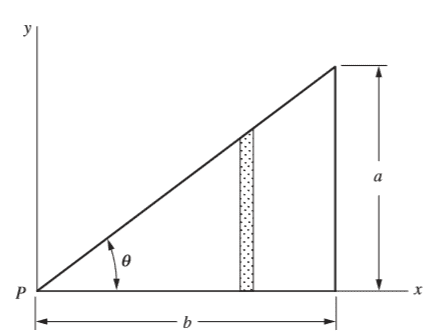
The right triangle shown with vertex P at the origin has base b, altitude a, and uniform density of surface charge σ. Determine the potential at the vertex P. First find the contribution of the vertical strip of width dx at x. Show that the potential at P can be written as $$\phi_P= (σb/4π \varepsilon_o)ln[(1+sinθ)/cosθ]$$

What I have done so far:

A tiny box of the strip has width dx and height $$rd\theta$$ so its contribution to P is
\begin{equation}
d\phi = \frac{(\sigma)(dx)(rd\theta)}{4 \pi \varepsilon_o r}=\frac{(\sigma)(dx)(d\theta)}{4 \pi \varepsilon_o }
\end{equation}
So the contribution of the entire strip would be
\begin{equation}
\frac{\sigma dx}{4 \pi \varepsilon_o}\int_0^{arctan(\frac{a}{b})} d\theta = \frac{\sigma dx}{4 \pi \varepsilon_o} arctan(\frac{a}{b})
\end{equation}
So the potential, $$\phi$$ would be:
\begin{equation}
\phi = \frac{\sigma}{4 \pi \varepsilon_o} arctan(\frac{a}{b}) \int_0^b dx = b\frac{\sigma}{4 \pi \varepsilon_o} arctan(\frac{a}{b})
\end{equation}
But this is clearly not the answer. What am I doing wrong?

 

[kuruman]

Look at the drawing. Angle θ is fixed, so dθ has no meaning here. The height of the strip is better represented as y and the area element as dA = y dx. Then express y in terms of x (it's a straight line) and integrate. Of course, first you need to find the potential of a line of charge of length y at perpendicular distance x from one of its ends.

 

[TSny]

A tiny box of the strip has width dx and height $$rd\theta$$

As kuruman pointed out, $\theta$ is a fixed angle.

Maybe you were thinking of using a variable angle $\varphi$, say, as shown in the attached figure below.
But, note that the height, $dy$, of the small box is not equal to $r d\varphi$.

Can you see how to express $dy$ in terms of $r d\varphi$ and an appropriate trig function of $\varphi$? If so, then you can let the integration variable for the vertical strip be $\varphi$ and it should simplify nicely.

 

[ramzerimar]

You probably could see the area of your element as dydx and integrate your potential function over the entire surface (one tip: try using polar coordinates).