How Do Electron and Proton Accelerations Compare Between Charged Plates?

[Sj4600]

Homework Statement

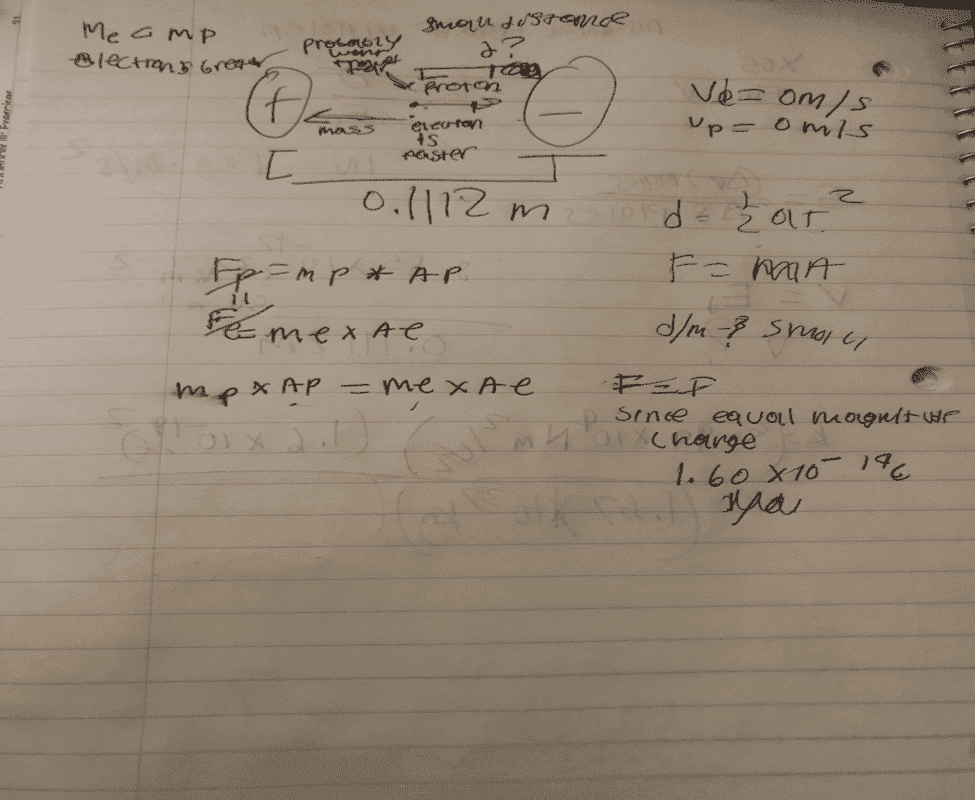
The plate separation of a charged capacitor is 0.1112 m. A proton and an electron are released from rest at the midpoint between the plates. Ignore the attraction between the two particles, and determine how far the proton has traveled by the time the electron strikes the positive plate.

Relevant Equations

d= 1/2at^2
F=MA

Ve=0m/s
Vp= 0m/s
Qe/Qp= 1.60E-19
Me=9.11E-31
Mp-1.67E-27

Ive pretty much gathered all of the equations I think I need to solve the problem. I just am stuck. The last step I realize that the forces would be equal to each other so I have mp x ap = me x ae but then when I try to solve for the accelerations. overall I am confused. I have also included some work that I've done

 

[archaic]

If you write the equation of motion of the electron, can you find out when it reaches the plate?
Given that result, and using its equation of motion, can you find out the distance the proton has traveled up to that instant?

 

[Sj4600]

the equation of motion of electron would be 1/2at^2 right ? and how do we know the acceleration and time ?

 

[archaic]

the equation of motion of electron would be 1/2at^2 right ? and how do we know the acceleration and time ?

Yes. Now, suppose that the electron reaches the plate at time $t$, then the distance traveled $\frac12at^2=?$ Once you figure that out, can you solve for the time?

Start by solving the problem using $a_e$ and $a_p$ like that. You will be able to use the relation you derived at the end.

 

[vela]

How do we know the acceleration and time ?

You won't be able to find a numerical result for either based on the information given, but you don't need to know them because the answer to the problem turns out to be independent of them. Mathematically, they would cancel out somewhere along the way. Generally, you won't always know when this will happen. Sometimes you just have to proceed algebraically for a while and hope for the best.

 

[Sj4600]

Ah yess I got it. simplified equations
a1*t^2/2 = s1 and a2*t^2/2 = s2.
so s1/a1=s2/a2
so s1/s2=a1/a2 = 5.45e-4.
where s2=0.1112/2
so s1=0.1112*5.45e-4/2=-->3.03E-5(m)

Thank you for you help!

 

[haruspex]

Generally, you won't always know when this will happen. Sometimes you just have to proceed algebraically for a while and hope for the best.

Then again, sometimes it is predictable, such as by dimensional analysis.
In the present case, the net force on the electron-proton system is zero, so the common mass centre doesn't move.
Note this means it is unnecessary to ignore the force between the particles.

 

[archaic]

Ah yess I got it. simplified equations
a1*t^2/2 = s1 and a2*t^2/2 = s2.
so s1/a1=s2/a2
so s1/s2=a1/a2 = 5.45e-4.
where s2=0.1112/2
so s1=0.1112*5.45e-4/2=-->3.03E-5(m)

Thank you for you help!

Well done, but I think that you should use 4 significant figures, since you have been given the distance like that.