Electric potential in a closed loop wire

[cupcake]

Homework Statement

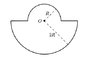
A closed loop of wire that has uniform linear density lambda is bent into the shape shown below, with dimension as indicated. Find the electric potential at point O, assuming it is zero at infinity. (see the attachment)

Homework Equations

V = k q /r

The Attempt at a Solution

Honestly, I am not sure how to attempt this question.
so far, what I did is.. I divided this loop into two part.

for part 1
dV = 2k lambda \int sin theta d(theta), which integral goes from 0 to 90 degree.
and after calculation, it gave me 2klamda with lambda is equal to q/pi*r.

but, I think there's something wrong here.., I don't know what to do..
please enlighten me..

the correct answer should be 2klambda ( pi + ln 2)

 

[Cyosis]

Why would you divide the loop into two parts, greatly decreasing the symmetry of the problem thus making it more difficult. A loop is as good as it gets. You have dV=k dq/r, dq=lambda dl, with dl an infinitesimal piece of the loop. Since we're at the center of the loop r is the same everywhere so r is constant. Therefor V becomes V=lambda k/r \int dl. What is \int dl?

 

[cupcake]

\int dl is \int pi r dr from r to 2r ?

 

[Cyosis]

I could have sworn that picture wasn't there before. Either way this changes things a bit. You will have to cut this configuration into four pieces. The two semi circles and the two straight sections. Let's look at the semi circle with radius R. First find out what is constant in the formula, dV=k dq/r. Is r constant? dq=lambda dl, how can you express the length of an arc of the loop in terms of the angle theta and the radius r?