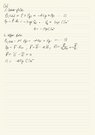Electromagnetics: find D,E,P between two parallel conducting plates

[larginal]

Homework Statement

Two infinite, parallel, perfectly conducting plates of a negligible thickness intersect the z-axis at right angles at z= 0.2 m and z = 0, carrying uniform charge densities p(surface charge density) = 45 * 10^-6 and -45*10^-6 respectively. the lower half of the space(0 <z<1) is filled with a dielectric of epsilon r = 1.5 , and the upper half of the space (0.1 < z < 0.2) is the air, epsilon r = 1.
when the lower plate is maintained at potential V = 0,
find
(a) D, E, P and V in the region 0 < z < 0.2 m
(b) total surface charge density on each plate.

Relevant Equations

D = epsilon0 * E + P

I tried to solve this problem on my own, but I'm not sure whether I solved correctly or not.
it is electromagnetics homework from my Uni, and it is pretty tough for me.
I attached the image of the problem and how I tried to solve this one.
I hope somebody will give some feedback.

 

[TSny]

If possible, please type in your work rather than post photos of your work. It makes it easier to read and easier to quote specific parts of your work.

In using Gauss' law in the form $\oint \mathbf{D} \cdot \mathbf{dS} = \large \frac{Q_{\rm enclosed}^{\rm free}}{\varepsilon_0}$, the $\mathbf{D}$-field appearing in the integral is the field due to all of the charge in the system. So, when you used the blue Gaussian surface to find $\mathbf{D}$, you found the net field due to all of the charge. When you used the red Gaussian surface, you just found the same field by a different choice of Gaussian surface. You should not add the $\mathbf{D}$'s for the two methods.

When you integrated $\mathbf{E} = -\boldsymbol{\nabla} V$ to find $V$, you need to take into account that $\mathbf{E}$ in the air is different than $\mathbf{E}$ in the dielectric.

Otherwise, I think you have the correct approach to the problem.