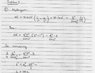What is the Size of the Box for an Electron Transition?

[warfreak131]

Homework Statement

I have a test in my physics class on tuesday, and as a study guide, our professor gave us a sample test and the solutions. I worked through most of it, except for this one question. I don't understand his method to solving it, I was hoping you guys had a solution. I have already email him about it, but he has yet to answer.

When an electron decays from the n=2 state to the n=1 state, it emits a photon. Determine the size of the box, L, for which the energy of this photon equals the energy of the analogous n=2 to n=1 transition in hydrogen.

The Attempt at a Solution

HIS attempt at the solution is in the attached jpeg.

I understand the process of finding the energy of the photon, that's very easy, but in finding the size of the box, he introduces this pi² term, and instead of doing the 1/n² - 1/m², he simply does n²-m²

 

[diazona]

Are you familiar with the infinite square well? That's the box your professor is talking about.

 

[issacnewton]

I understand the process of finding the energy of the photon, that's very easy, but in finding the size of the box, he introduces this pi² term, and instead of doing the 1/n² - 1/m², he simply does n²-m²

Your professor is considering the energy levels for a particle in a box. look here

[PLAIN]http://en.wikipedia.org/wiki/Particle_in_a_box

[/PLAIN]

For one dimensional box of length L, the energy levels are

E_n=\frac{n^2\hbar^2 \pi^2}{2mL^2}

so

\Delta E=E_2-E_1=\frac{\hbar^2 \pi^2}{2mL^2}(2^2-1^2)

 

[warfreak131]

Are you familiar with the infinite square well? That's the box your professor is talking about.

Yes, but I'm still not sure what he's doing.

 

[warfreak131]

Your professor is considering the energy levels for a particle in a box. look here

[PLAIN]http://en.wikipedia.org/wiki/Particle_in_a_box

[/PLAIN]

For one dimensional box of length L, the energy levels are

E_n=\frac{n^2\hbar^2 \pi^2}{2mL^2}

so

\Delta E=E_2-E_1=\frac{\hbar^2 \pi^2}{2mL^2}(2^2-1^2)

ooooo, i see.

thanks!