A13235378
- 50
- 10
- Homework Statement
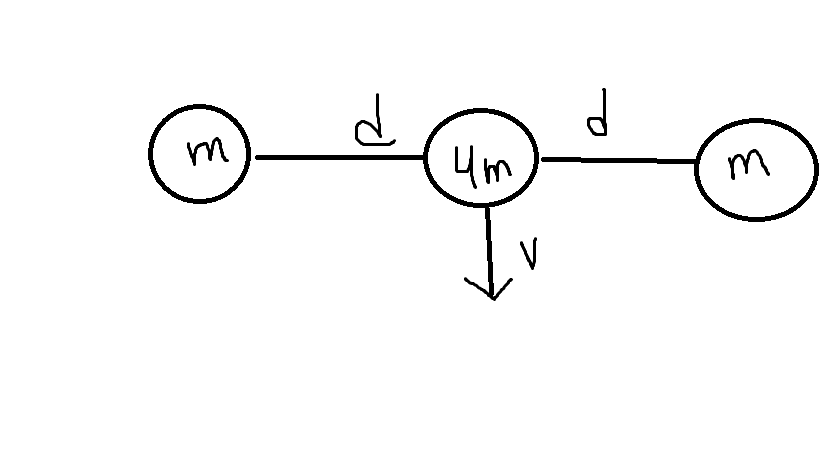
- Three small metallic balls, loaded with q charges, have masses equal to m, 4m and m. The balls are connected by insulating wires of each length and placed on a horizontal table without friction. Initially the balls are at rest in a straight line as shown. Then a quick horizontal push gives the central ball a velocity v directed perpendicular to the strings. Find the subsequent minimum distance D between the balls of dough m.
- Relevant Equations
- Q=mv (amount of moment)
E= Qq/4πex (potential energy)
I did energy conservation,
considering that the final velocity of the largest mass would be zero and I used moment conservation. But
I am not finding the answer . Where I maked a mistake?
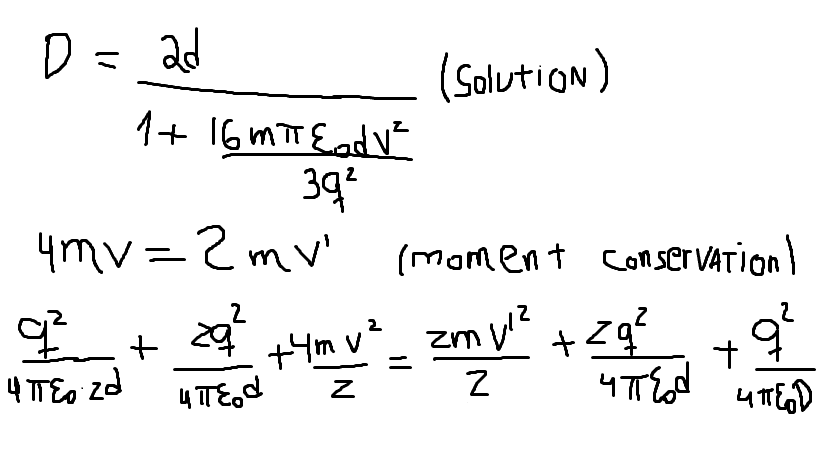
considering that the final velocity of the largest mass would be zero and I used moment conservation. But
I am not finding the answer . Where I maked a mistake?