- #1
daniel444
- 5
- 1
what is the reason for that the energy hypersurfaces in a phase space, which belong to systems with constant energy are closed? ( see picture )
Energy hypersurface in a phase space (statistical physics)
- Context: Graduate
- Thread starter daniel444
- Start date
Click For Summary
SUMMARY
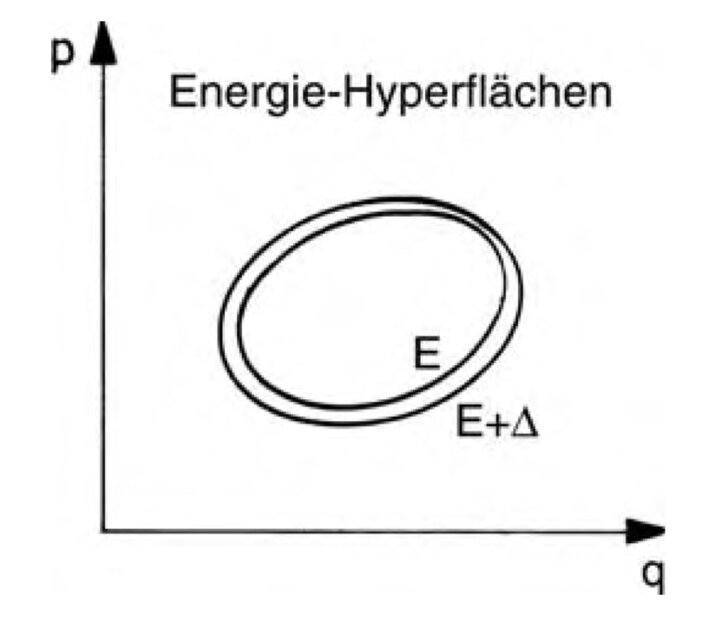
The energy hypersurfaces in a phase space for systems with constant energy are inherently closed due to the necessity of defining boundaries between regions of differing energy levels. This closure ensures the existence of energy contours, which are critical for the establishment of gradients and forces within the system. Without closed hypersurfaces, the distinction between higher and lower energy regions would be lost, leading to a breakdown in the fundamental principles of statistical physics.
PREREQUISITES- Understanding of phase space concepts in statistical mechanics
- Familiarity with energy hypersurfaces and their properties
- Knowledge of gradients and forces in physical systems
- Basic principles of thermodynamics
- Explore the mathematical formulation of phase space in statistical mechanics
- Study the implications of closed energy hypersurfaces on thermodynamic systems
- Investigate the role of energy contours in defining physical forces
- Learn about the relationship between energy hypersurfaces and stability in dynamical systems
Researchers in statistical physics, physicists studying thermodynamic systems, and students seeking to understand the implications of energy hypersurfaces in phase space analysis.
Similar threads
Undergrad
Statistical ensemble in phase space
- · Replies 29 ·
- · Replies 7 ·
- · Replies 15 ·
- · Replies 16 ·
- · Replies 3 ·
- · Replies 1 ·
- · Replies 6 ·
- · Replies 10 ·
- · Replies 3 ·
- · Replies 9 ·