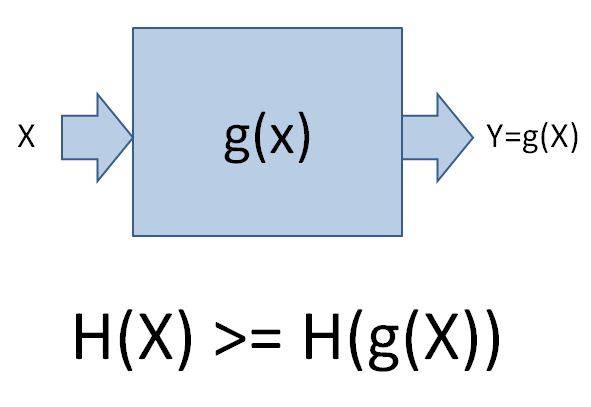
That law only applies if x is the only argument of that function.
Let's assume x is the state of the universe and g is the laws of physics applied over a specific amount of time. Then g(x) will be the future state of the universe.
However the increase in entropy happens because of quantum randomness, that means our function g needs a second argument R which is a source of randomness. So you then have g(x, R).
That's if x is the state you measure with some instruments i.e. a classical state.
If on the other hand you look at a pure quantum system without any measurements or wave function collapse then there is no randomness and you just have g(x). But in such a case there is also no
change in entropy/information. Conservation of information is a basic law of quantum mechanics.