KyleTS
- 4
- 1
< Mentor Note -- thread moved to HH from the technical math forums, so no HH Template is shown >[/color]
This is from the question list at the UC Davis Website epsilon delta exercise list.
In the exercise list we have:
Prove that
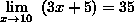
Which concludes with:
Thus, if
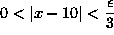 , it follows that [PLAIN]https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/preclimsoldirectory/img13.gif. This completes the proof.
, it follows that [PLAIN]https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/preclimsoldirectory/img13.gif. This completes the proof.
My curiosity is here: This concludes with iff-then rhetoric. IFF ,
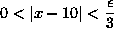 THEN [PLAIN]https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/preclimsoldirectory/img13.gif. Which is true here as was proven. However, I don't see anything which explicitly demonstrates that for all real ε>0 with ε/3, there is an x in the domain of f(x), such that [PLAIN]https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/preclimsoldirectory/img20.gif. This seems intuitively obvious, and likely easy to demonstrate in this case, however if the δ = (function of ε) is sufficiently complex, it seems as though verifying 0 < |x-10| < δ may require another epsilon-delta proof itself. That is to say, the proof here does show that IFF, THEN, however I don't see anything which demonstrates the IFF is actually true.
THEN [PLAIN]https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/preclimsoldirectory/img13.gif. Which is true here as was proven. However, I don't see anything which explicitly demonstrates that for all real ε>0 with ε/3, there is an x in the domain of f(x), such that [PLAIN]https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/preclimsoldirectory/img20.gif. This seems intuitively obvious, and likely easy to demonstrate in this case, however if the δ = (function of ε) is sufficiently complex, it seems as though verifying 0 < |x-10| < δ may require another epsilon-delta proof itself. That is to say, the proof here does show that IFF, THEN, however I don't see anything which demonstrates the IFF is actually true.
Have I missed something here? Thanks in advance, everyone!
This is from the question list at the UC Davis Website epsilon delta exercise list.
In the exercise list we have:
Prove that
Which concludes with:
Thus, if
My curiosity is here: This concludes with iff-then rhetoric. IFF ,
Have I missed something here? Thanks in advance, everyone!
Last edited by a moderator: