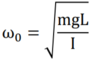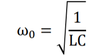SUMMARY
This discussion focuses on demonstrating the equations governing simple harmonic motion in a physical pendulum and an LC circuit. The key formulas include the equation of motion for the pendulum, represented as ##\tau_z = I_z \ddot{\theta}_z##, and Kirchhoff's law for the LC circuit. Participants emphasize the importance of showing initial efforts in problem-solving before receiving assistance. Additionally, they suggest exploring the relationship between the coefficients in the differential equations of both systems to deepen understanding.
PREREQUISITES
- Understanding of simple harmonic motion
- Familiarity with the equation of motion for a physical pendulum
- Knowledge of Kirchhoff's laws in electrical circuits
- Basic differential equations
NEXT STEPS
- Research the derivation of the equation of motion for a physical pendulum
- Study Kirchhoff's voltage law and its application in LC circuits
- Learn about energy conservation in mechanical systems and electrical circuits
- Explore the relationship between natural frequency and system parameters in oscillatory systems
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and electrical circuits, as well as educators seeking to enhance their teaching of simple harmonic motion concepts.