dawo0
- 5
- 0
Homework Statement
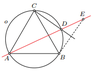
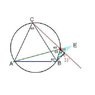
Can someone help me solve this, and teach me how to solve such problems in future? An equilateral triangle ABC is inscribed in a circle . Point D lies on a shorter arc of a circle BC. Point E is symmetrical the point B relating to the line CD . Prove that the points A, D , E lie on one straight line. If something is unclear just tell me.
Homework Equations
--------
The Attempt at a Solution
I do not know how to go about Himself .
Frame I figure .