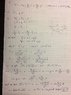SUMMARY
The discussion centers on determining the stability of electric charge equilibrium using the equation x² + 3x - 0.45 = 0, which yields solutions x₁ = 0.14 and x₂ = -3.14. The first derivative, f' = 2x + 3, indicates that f'(x₁) > 0, confirming that the charge at x₁ is stable. Participants debated the correct interpretation of equilibrium and stability, emphasizing the need for a clear understanding of Coulomb forces and the placement of charges along the x-axis.
PREREQUISITES
- Understanding of electric charge interactions and Coulomb's law
- Knowledge of calculus, specifically first derivatives
- Familiarity with quadratic equations and their solutions
- Ability to interpret force fields and equilibrium in physics
NEXT STEPS
- Explore the concept of electric field strength and its calculation
- Study the implications of stability in electric charge systems
- Learn about graphical representations of force fields in electrostatics
- Investigate the effects of varying charge magnitudes on equilibrium positions
USEFUL FOR
Students and educators in physics, particularly those focusing on electrostatics, as well as anyone involved in solving problems related to electric charge equilibrium and stability.