ChessEnthusiast
- 115
- 3
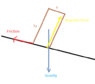
We have a cube on an inclined plane.
The tipping condition is the presence of an unbalanced torque relative to the center of mass (contributing forces are: the normal force and the force of friction).
However, is this conditions equivalent to the previous one:
The line of action of the force of gravity points outside the base of the cube AND the force of friction is large enough to prevent the cube from sliding?
If not, it it easy to think of a simple counterexample?
The tipping condition is the presence of an unbalanced torque relative to the center of mass (contributing forces are: the normal force and the force of friction).
However, is this conditions equivalent to the previous one:
The line of action of the force of gravity points outside the base of the cube AND the force of friction is large enough to prevent the cube from sliding?
If not, it it easy to think of a simple counterexample?