Estimating Pool Area Using Simpson's Rule

[bns1201]

I put this in the homework section a few days ago, but the homework was already due, and I'd like an explanation as to how to do this please. I have a feeling a similar problem will be on the exam.

The widths (in meters) of a kidney-shaped swimming pool were measured at 2 meter intervals as indicated in the figure. Use Simpson's Rule to estimate the area of the pool. Please round the answer to the nearest square meter.

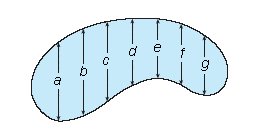
a = 5.8
b = 6.6
c = 5.4
d = 5.8
e = 5.2
f = 4.8
g = 5.2



Thanks

 

[mathman]

I am assuming that a and g were each 2 meters from the edge.
Then Simpson's rule gives 4(4a+2b+4c+2d+4e+2f +4g)/6.