Another
- 104
- 5
- Homework Statement
- I am wondering about definition of a function
- Relevant Equations
- ## F = \frac{(1+(y_x)^2)^{\frac{1}{2}}}{(y_1-y)^{\frac{1}{2}}}##
My question : I am wondering about definition of a function. when ##y_x = (\frac{b+y}{a-y})^2##
Why in this book is defined solution ##y = y(x)## in from ## y = y(θ(x))## . And have a relationship in the form
## y = \frac{1}{2} (a-b) - \frac{1}{2} (a+b) cosθ ## ?
_____________________________________________________________________________________________________________________________________
In this book is defined ## F = \frac{(1+(y_x)^2)^{\frac{1}{2}}}{(y_1-y)^{\frac{1}{2}}}##
The E-L equation in case F = ##F(y,y_x)## ===> ##F - y_x \frac{∂F}{∂y_x} = c## when c is constant.
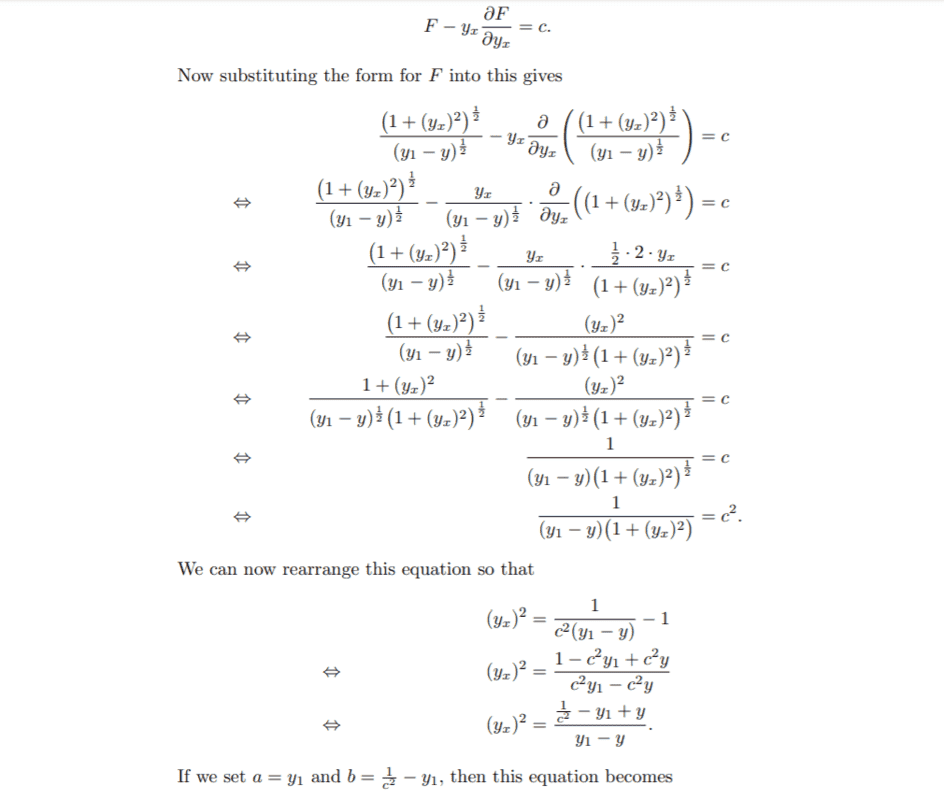
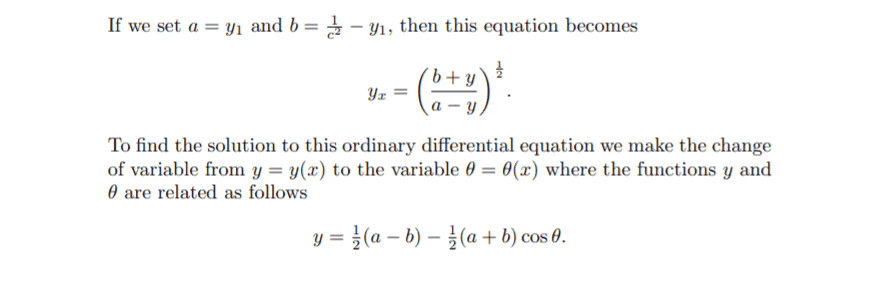
Why in this book is defined solution ##y = y(x)## in from ## y = y(θ(x))## . And have a relationship in the form
## y = \frac{1}{2} (a-b) - \frac{1}{2} (a+b) cosθ ## ?
_____________________________________________________________________________________________________________________________________
In this book is defined ## F = \frac{(1+(y_x)^2)^{\frac{1}{2}}}{(y_1-y)^{\frac{1}{2}}}##
The E-L equation in case F = ##F(y,y_x)## ===> ##F - y_x \frac{∂F}{∂y_x} = c## when c is constant.