Euler Lagrange Equations for simple multi-body systems

[Trying2Learn]

TL;DR Summary

Examples needed.

Good Morning (or afternoon)

I am in search of real-world examples of the use of Euler-Lagrange equations.

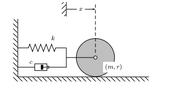
I post several examples below. These are the ones I do NOT want

You see, I think that idealized problems primarily teach problem-solving mechanics, and I take no umbrage with that; however, they can feel disconnected from real applications.

It would be nice to find a source of problems that stated that the mechanisms below are important, but not just for idealized problems. I am looking for a source that says....

"Now this problem below, is an idealiztion of a propellers, motorcycle with passenger, elevator lift, or so on. And evne provides a few words on why the particular schematic is important (beyond just practicing skills).

Does it make sense.... what I am asking for?

Like below, on the left: this is what happens when wet clothes clump up in a washing machine.

 

[Juanda]

I feel you. Sometimes textbooks seem detached from reality. I understand they're trying to build your skills and throwing real problems at you often makes things too complicated because reality is complex. But that's where professors must come in and introduce the necessary simplifications that still keep the subject relevant.

There are some mechanisms that are somewhat simple and can be studied at different levels of detail. For example:

https://en.wikipedia.org/wiki/Kinematic_diagram

I'd say it's better to spend a long time with the same mechanism going deeper and deeper as you get more familiar with the analytical tools you're using.

This is how I'd try to teach this subject. First of all, I'd arm myself with virtual 3D models, simulations with all the relevant graphs, and actual mechanical parts (3D printing made this very easy) to show during the classes to relate to each of the following points.

• Get a conceptual understanding of the mechanism.
• Its applications. Often favored by a chronological approach. Since that's how humanity came to understand the mechanism, I feel it's a very intuitive way to teach and learn too. I'd say it applies to almost any concept in math and physics although there are clear benefits to adapting and simplifying the language and math used. Reading Philosophiæ Naturalis Principia Mathematica by Newton the way it was originally written can't be a too fun experience although I can't really tell since I haven't done it myself.
• Describing its motion using different tools such as Newton and Lagrangian mechanics to see the benefits of each.
• Analyzing the inertial forces appearing as a result of its rotation.
• Solving a design problem with a defined target. I think design problems really make a difference when trying to understand a concept. In reality, it'll be your job to define the target, solve the problem, and then optimize the solution. This is a skillset rarely seen taught in universities (in the 3 I have studied at least). Instead, we're taught to solve problems with very well-predefined conditions and solutions because it makes teaching more manageable. A few problems related to that mechanism out of the top of my head:
  • For $L_3$ being defined, obtain the length $L_2$ so that the stroke is $L_s$.
  • For the constrained space defined by the coordinates $y_A$ and $y_B$, calculate the bodies $L_2$ and $L_3$ so the stroke is confined in that space.
  • Optimize the problem so that...
  • Etc. As you get more experience, the problem will be more general and you'll be the one defining the targets.
• Seeing how complexity increases as more pistons are added and for what purpose it's done.
• Applications in 3D mechanism and challenges.
• Brief overview of state of the art.

As you can see, a simple mechanism can already give you quite a lot of insight into math, physics, and the real world. However, this approach is not often seen in universities where there are a lot of different things being cramped together and too little time to see them all.
In my opinion, this kind of approach is worth it even if you have to cut other things from the lessons. Regarding teaching, I have only worked as an assistant teacher to individuals or very small groups with most alumni being high schoolers so maybe more experienced professors from this forum will differ.