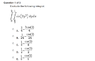SUMMARY
The integral discussed is \int_0^2 \int_{x/2}^1 sin(2y^2) \, dy \, dx. The solution involves switching the limits of integration and integrating first with respect to y before x. The final result of the evaluation is -1/2 + cos(2)/2. The discussion highlights the importance of understanding dummy variables in integration and the necessity of correctly interpreting the limits of integration.
PREREQUISITES
- Understanding of double integrals in calculus
- Familiarity with the concept of dummy variables in integration
- Knowledge of trigonometric integrals, specifically
sin(2y^2)
- Experience with changing limits of integration
NEXT STEPS
- Study the process of switching limits in double integrals
- Learn techniques for integrating trigonometric functions, particularly
sin(2y^2)
- Explore graphical methods for visualizing integration boundaries
- Review u-substitution and its limitations in integral calculus
USEFUL FOR
Students studying calculus, particularly those working on double integrals and integration techniques, as well as educators seeking to clarify concepts related to limits of integration and dummy variables.