Sciencestd
- 60
- 9
If we look to the figure, in several articles they mentioned that the part of the mode field, the tail of the mode field diameter, travel in the cladding, this maybe I can understand that because of a little change between the refractive indices of the core and the cladding, then the transverse mode field will encounter less change. Then they mentioned that the other side they took off the cladding so now let say it is air, then the length of the evanescent field in that side obey to the equation as in the second picture, and the field is rapidly decaying... Why?! What is the physical reason? which equations include that? why should the transvers part changed to this situation?
Images source: https://www.researchgate.net/publication/44067714 and scirp.org
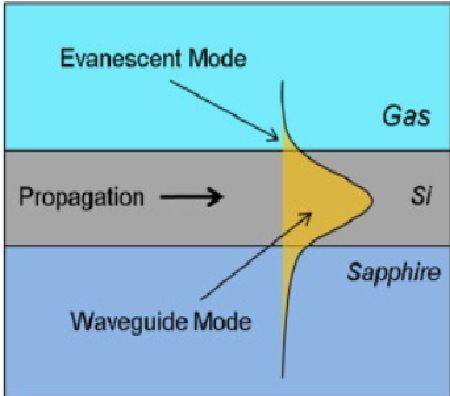
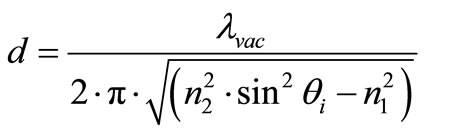
Images source: https://www.researchgate.net/publication/44067714 and scirp.org