Excess pressure inside a Liquid drop

[Vivek98phyboy]

While studying about the effects of surface tension i came across the excess pressure inside a liquid drop.
Here they considered a hemisphere ABCDE from the drop and listed out the conditions for it to be in equilibrium.

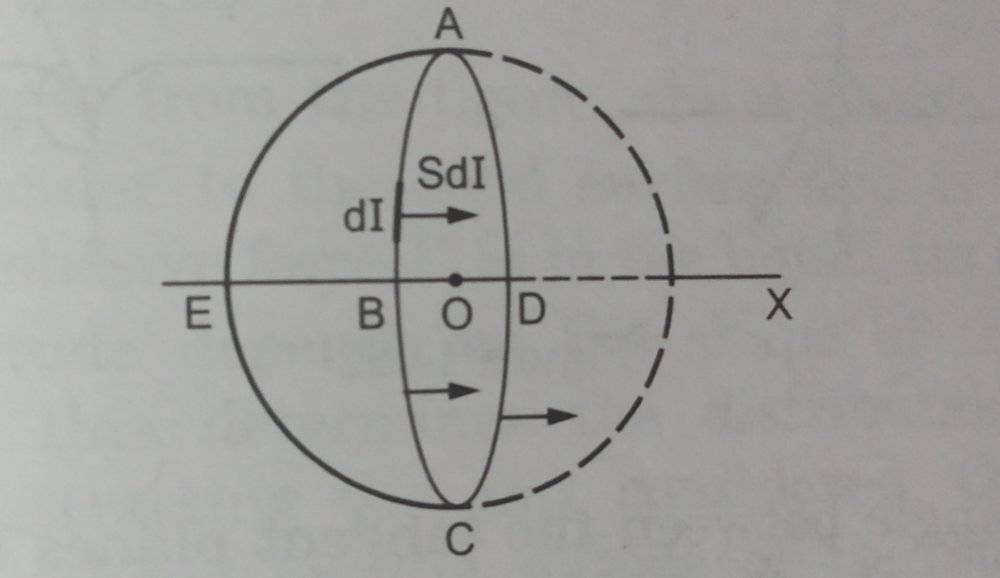
The forces acting on them are taken as

F1= 2πRS
F2= P1×(Projection of hemispherical surface on ABCD)
=>F2=P1×πR²
F3=P2×πR²

For equilibrium we take
F1+F2=F3

But what role does the surface tension (T) has in maintaining the equilibrium for a hemisphere.
My doubts are:
1. Isn't the pressure due to Atmosphere and the pressure inside the hemispherical drop enough to balance each other. Why do we need a surface tension here?
2. When i referred some other sources, it said that the surface tension holds the drop from bursting. If it is so, the force due to T we calculates here acts only along the base periphery of the hemisphere. What effect would it have on the curved surface?

Hope this won't come under Homework help

 

[gleem]

The surface tension of the bubble is due to the attraction of molecules with their neighbors thus pulling them closer and causing the surface area to shrink. This naturally will increase the pressure inside until an equilibrium situation is produced.

In the analysis three forces are identified. That due to the outside pressure pushing on the surface (P₀πr²) that due to the surface tension acting in the surface on the circumference (2π rσ) which act together and that due to the inside pressure (P πr²) countering the other two to produce the equilibrium situation. where r is the radius and σ is the surface tension

The pressure in the bubble is constant throughout . The splitting of the bubble into two hemispheres simplifies the analysis.

thus

P πr² = P₀πr² + 2π rσ

or P = P₀+ 2σ/r

 

[Vivek98phyboy]

The surface tension of the bubble is due to the attraction of molecules with their neighbors thus pulling them closer and causing the surface area to shrink. This naturally will increase the pressure inside until an equilibrium situation is produced.

In the analysis three forces are identified. That due to the outside pressure pushing on the surface (P₀πr²) that due to the surface tension acting in the surface on the circumference (2π rσ) which act together and that due to the inside pressure (P πr²) countering the other two to produce the equilibrium situation. where r is the radius and σ is the surface tension

The pressure in the bubble is constant throughout . The splitting of the bubble into two hemispheres simplifies the analysis.

thus

P πr² = P₀πr² + 2π rσ

or P = P₀+ 2σ/r

What if the surface tension is zero?
How would the hemispherical part of the drop behave?

 

[Lord Jestocost]

What if the surface tension is zero?

Regarding zero surface tension:
Does an ideal fluid have zero surface tension? | Physics Forums

 

[Vivek98phyboy]

Regarding zero surface tension:
Does an ideal fluid have zero surface tension? | Physics Forums

It said cohesive and adhesive forces would be the same. Does that mean they would behave like gas molecules?

 

[Lord Jestocost]

See comment #2 by @.Scott in the thread:

Zero surface tension: "It would signify that the molecules within the fluid have the same attraction to each other as to the atmosphere at the surface."