member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Newton Second Law
I am trying to verify Newton II. The setup I am using is,
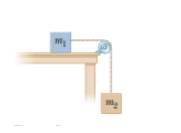
Where ##m_1 = 0.887 kg## is a cart and ##m_2 = 0.02016 kg## is a small hanging mass. There is a force sensor on ##m_1## to measure the force acting on it from the string and the acceleration of the cart.
To verify Newton's Second Law, we tried to plot we plot acceleration of ##m_2## vs force ##F## which is the same as the tension ##T##.
Apply Newton II to the ##m_2##: ##T = m_2a + m_2g## which is a linear equation (##y = mx + c##) of the form,
which is of the form ##y = T, m = m_2, x = a## and ##c = m_2g##
Therefore we graphed T vs a to get:
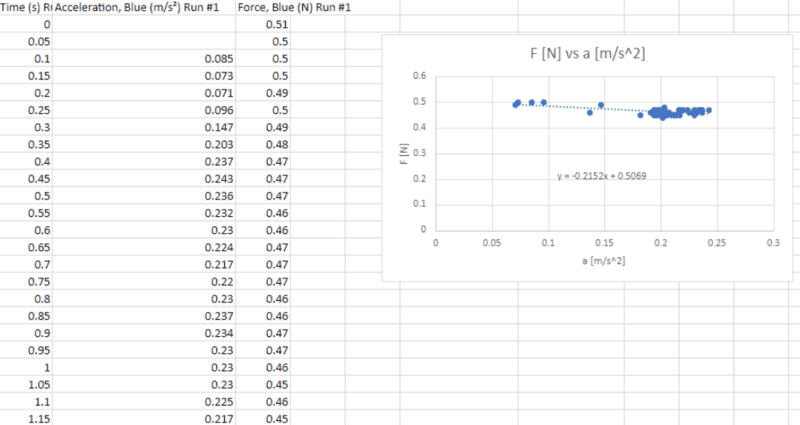
However, do you please know why I am getting ##m_2 = -0.2152 kg## from the graph when we measure it to be 0.02kg? I am not sure why the negative sign and why it is x10 larger than the measured ##m_2##. Also when I solve ##c = 0.5069 = m_2g##, for ##m_2## I also get a very different value for ##m_2##
Any help greatly appreciated!
Many thanks!
Where ##m_1 = 0.887 kg## is a cart and ##m_2 = 0.02016 kg## is a small hanging mass. There is a force sensor on ##m_1## to measure the force acting on it from the string and the acceleration of the cart.
To verify Newton's Second Law, we tried to plot we plot acceleration of ##m_2## vs force ##F## which is the same as the tension ##T##.
Apply Newton II to the ##m_2##: ##T = m_2a + m_2g## which is a linear equation (##y = mx + c##) of the form,
which is of the form ##y = T, m = m_2, x = a## and ##c = m_2g##
Therefore we graphed T vs a to get:
However, do you please know why I am getting ##m_2 = -0.2152 kg## from the graph when we measure it to be 0.02kg? I am not sure why the negative sign and why it is x10 larger than the measured ##m_2##. Also when I solve ##c = 0.5069 = m_2g##, for ##m_2## I also get a very different value for ##m_2##
Any help greatly appreciated!
Many thanks!