How Does Momentum Transfer Relate to Spherical Symmetry in Form Factors?

[malawi_glenn]

I have a form factor that only depends on the momentum transfer q, this is symbolised by writing the form factor as F(B]q[/B]^2).

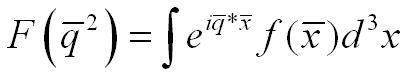
if i have a spherical symmetric distribution of charge, f only depends on the radius; r = | q|

Then integration over all solid angels yields:

https://www.physicsforums.com/attachment.php?attachmentid=9530&stc=1&d=1174376003

(there should be a r^2 inside the integral ;))

I do not understand how this Sinus - thing plops up.. all i know is this:
https://www.physicsforums.com/attachment.php?attachmentid=9531&stc=1&d=1174376117

I really need a hint how to go from the exponential function to this sinus thing. =/

 

[Dick]

Since f(x) is independent of the polar angles you can rotate the x coordinate system so that the q vector points along, say, the positive z-axis. So the exponential becomes exp(i*|q|*r*cos(theta)). Doing the theta integration gives you the 'sinus thing'.

 

[malawi_glenn]

thanx a lot, i will try tonight:)

 

[malawi_glenn]

it was a piece of cake now, thanks again!

 

[Irene Sh.]

Could you explain more about it?