Express rectangle area as function of x

In summary, expressing rectangle area as a function of x means finding a mathematical relationship between the length and width of a rectangle and its area. This is useful in various fields and can be done using the formula A = x * w or A = x * l, where x represents the length or width of the rectangle and w or l represent the width or length. This formula can be applied to any type of rectangle, regardless of its regularity.
  • #1
kbillsy
2
0
Hey so another expressing functions question:

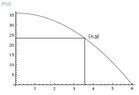
A rectangle has on corner on the graph of y=36-x^2, another at the origin, a 3rd on the positive y-axis, and the fourth on the positive x-axis. Express the area A of the rectangle as a function of x. What is the domain of A? For what value of x is A largest?
 
Mathematics news on Phys.org
  • #2
Let's look at a diagram:

View attachment 2132

In terms of $x$, what is the base of the rectangle...what is its height?
 

Attachments

  • kbillsy.jpg
    kbillsy.jpg
    5.6 KB · Views: 70

FAQ: Express rectangle area as function of x

What does it mean to express rectangle area as a function of x?

Expressing rectangle area as a function of x means finding a mathematical relationship between the length and width of a rectangle (represented by x) and its area. This allows us to calculate the area of a rectangle for any given value of x.

Why do we need to express rectangle area as a function of x?

Expressing rectangle area as a function of x can be useful in various fields such as engineering, physics, and economics. It allows us to analyze and make predictions about the relationship between the dimensions of a rectangle and its area.

How do you express rectangle area as a function of x?

To express rectangle area as a function of x, we use the formula A = x * w where A represents the area and w represents the width of the rectangle. We can also express it as A = x * l where l represents the length of the rectangle. Both formulas are equivalent and can be used interchangeably.

What are the variables in the formula for expressing rectangle area as a function of x?

The variables in the formula for expressing rectangle area as a function of x are x (representing the length or width of the rectangle) and w (representing the width) or l (representing the length). The value of x can vary, but w and l remain constant for a given rectangle.

Can we use this formula for any type of rectangle?

Yes, we can use this formula for any type of rectangle as long as we know the value of x and the length or width of the rectangle. This formula works for both regular and irregular rectangles.

Similar threads

MHB -gre.ge.11 x,y of fourth corner of diagonal
Replies
3
Views
1K
MHB Question about a rounded rectangle
Replies
1
Views
7K
MHB Khegan McLane's Math Problem: Rectangle Inscribed Between Parabola & X-Axis
Replies
1
Views
6K
MHB Find Perimeter of Rectangle with Given Area and Width
Replies
21
Views
3K
MHB Maximizing Area of Inscribed Rectangle - Yahoo Answers
Replies
1
Views
12K
How 'x' (multiplication) found its way into formula of area of rectangle?
Replies
6
Views
2K
MHB Andrew's question at Yahoo Answers regarding maximizing the area of a rectangle
Replies
1
Views
5K
MHB Geometry and Trigonometry Challenge
Replies
2
Views
1K
B Understanding exponentiation and logarithms together
Replies
12
Views
2K
I The Basic Area Problem (introduction to the topic of integrals)
Replies
24
Views
3K

Hot Threads

Recent Insights

Back
Top