Discussion Overview
The discussion revolves around expressing y(t) as a function of x(t) within the context of a homework problem. Participants explore transformations of the function and compare their results with a figure from a textbook.
Discussion Character
- Homework-related, Technical explanation
Main Points Raised
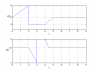
- One participant presents a transformation approach leading to the expression y(t) = -0.5x(2t-4)+1.5 and questions discrepancies with a textbook figure.
- Another participant suggests that the initial answer appears correct.
- A further participant notes that the time scale for the textbook figure remains unchanged for the interval 4 < t < 5, raising concerns about the validity of the comparison with their plot.
- Another participant agrees with the correctness of the initial transformation and expression.
Areas of Agreement / Disagreement
While some participants agree on the correctness of the transformation, there is uncertainty regarding the comparison with the textbook figure, indicating that multiple views remain on the interpretation of the results.
Contextual Notes
Participants express concerns about the time scale differences and how they affect the comparison between their plots and the textbook figure, highlighting possible limitations in the problem's setup.