Falling hailstones hitting two car windscreens

[DifferentialGalois]

Homework Statement

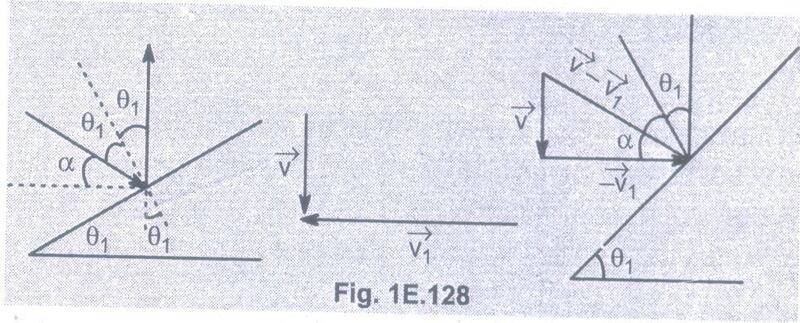
Two motor cars have their wind screens at $\theta_1=15^{\circ}$ and $\theta_2=30^{\circ}$ respectively. While moving in a hailstorm the drivers see the hailstones bounced by the wind screen of their cars in the vertical direction. What is the ratio $\dfrac{v_1}{v_2}$ of the velocities of the cars $?$ Assume the hailstorms fall vertically.

Relevant Equations

SEE HW STMENT

I tried to construct a diagram, but to no avail, since I don't really understand the qn. However, my professor provided me with this graphical depiction (that i obviously don't understand)

 

[erobz]

It's hard to tell which part of it you are not understanding without first showing some attempt.

 

[kuruman]

According to our rules, to receive help, you need to show some credible effort towards answering the question. How about telling us what kind of diagram you tried to construct and how you think it might have helped you.

Please read, understand and follow our homework guidelines, especially item 4, here
https://www.physicsforums.com/threads/homework-help-guidelines-for-students-and-helpers.686781/

 

[DifferentialGalois]

verbal explanation thus far:
Hailstones bounce in the vertical direction which implies that the angle of reflection is $\theta_1$ as shown in figure, which is same as angle of incidence in the cars' reference frame. Velocity of hailstones relative to the first car is $\dfrac{v_1}{v_2}$ as shown in the figure.

 

[haruspex]

verbal explanation thus far:
Hailstones bounce in the vertical direction which implies that the angle of reflection is $\theta_1$ as shown in figure, which is same as angle of incidence in the cars' reference frame. Velocity of hailstones relative to the first car is $\dfrac{v_1}{v_2}$ as shown in the figure.

There is some confusion in the subscripts.
Since the windscreen angle is drawn differently in the left and right diagrams I assume these are for the two cars, but both diagrams show $\theta_1, v_1$, both use $\alpha$ instead of $\alpha_1, \alpha_2$.
The speed of the hailstones relative to that of the first car is $\frac v{v_1}$, not $\frac{v_1}{v_2}$.

What is the relationship between $v, v_1, \alpha_1$?
What is the relationship between $\theta_1, \alpha_1$?

 

[DifferentialGalois]

There is some confusion in the subscripts.
Since the windscreen angle is drawn differently in the left and right diagrams I assume these are for the two cars, but both diagrams show $\theta_1, v_1$, both use $\alpha$ instead of $\alpha_1, \alpha_2$.
The speed of the hailstones relative to that of the first car is $\frac v{v_1}$, not $\frac{v_1}{v_2}$.

What is the relationship between $v, v_1, \alpha_1$?
What is the relationship between $\theta_1, \alpha_1$?

who knows? i hav no idea.

 

[haruspex]

who knows? i hav no idea.

Look at the right hand diagram. There is a triangle with sides labelled $v, v_1$ and an angle $\alpha$. What equation relates them, given that v is vertical and v1 horizontal?

Look at the left hand diagram. What is the angle between the horizontal dashed line and the vertical arrow? What angles lie between them?

 

[DifferentialGalois]

Look at the right hand diagram. There is a triangle with sides labelled $v, v_1$ and an angle $\alpha$. What equation relates them, given that v is vertical and v1 horizontal?

Look at the left hand diagram. What is the angle between the horizontal dashed line and the vertical arrow? What angles lie between them?

$\alpha + 2\theta_1=\frac{\pi}{2} and \tan{\alpha}-\dfrac{v}{v_1}$
but i still dont understand how they constructed that diagram.

 

[PeroK]

My first thought is that you will need a clear strategy. The velocities of the cars, presumably, are to be calculated in the ground frame. Whereas, the driver's observations are in their moving reference frames.

There's a lot to get straight before you can begin to solve this. Tricky, IMO.

 

[erobz]

but i still dont understand how they constructed that diagram.

There is some law about reflection at work in the cars frame of reference?

 

[PeroK]

There is some law about reflection at work in the cars frame of reference?

Which is another unstated assumption in the question.

 

[haruspex]

Fixing up your LaTeX and other details:

$\alpha_1 + 2\theta_1=\frac{\pi}{2}$ and $\tan{\alpha_1}=\dfrac{v}{v_1}$
but i still dont understand how they constructed that diagram.

The diagram is using a graphical way to add vectors.
The hail has a vertically down velocity of $v$. In car 1's frame of reference it also has a horizontal velocity to the right of $v_1$. Adding these two vectors gives the velocity of the hail relative to car 1.

 

[DifferentialGalois]

Fixing up your LaTeX and other details:

The diagram is using a graphical way to add vectors.
The hail has a vertically down velocity of $v$. In car 1's frame of reference it also has a horizontal velocity to the right of $v_1$. Adding these two vectors gives the velocity of the hail relative to car 1.

Alr could u provide me a solution. Then i'll be happy. Thank you sir.

 

[hutchphd]

No one else will be happy with that result.

 

[PeroK]

Alr could u provide me a solution. Then i'll be happy. Thank you sir.

I think you have a solution, but you don't understand it. The key point is that when we move to the car's reference frame, the velocity of the hailstones (in that reference frame) has the same vertical component ($v$) and also a horizontal component $-v_1$ or $-v_2$ respectively.

At this point you can analyse the scenario as if the car were stationary and the hailstones were being fired it at an angle with these velocity components.

A bit of trigonometry is needed to show that, if the windscreen is at an angle $\theta$ with the horizontal, then the angle of incidence of the hailstones is also $\theta$. Given that the hailstones bounce vertically in the car frame. This is the diagram you were given.

That's all you need to derive an expression for $\frac {v_1} v$ in terms of $\theta_1$ and the same for $v_2$.

You can then put these equations together to express the ration $\frac{v_1}{v_2}$ in terms of some trig function of $\theta_1$ and $\theta_2$.

The solution involves these four steps and the associated calculations. Can you identify which parts of this solution you do not understand?

 

[haruspex]

Alr could u provide me a solution. Then i'll be happy. Thank you sir.

Please try to identify the step you do not understand in post #12 or #15.

 

[DifferentialGalois]

Please try to identify the step you do not understand in post #12 or #15.

All the steps

 

[PeroK]

All the steps

If that is true, then the problem is too advanced for you at this stage. You should find some simpler problems and revise your trigonometry.

 

[DifferentialGalois]

If that is true, then the problem is too advanced for you at this stage. You should find some simpler problems and revise your trigonometry.

i mean i can treat it like a math problem, by writing down the logical conclusions:
$\tan{\alpha}=\tan{\left(\dfrac{\pi}{2}-2\theta_1\right)}-\cot{2\theta_1}$

𝑣/𝑣1=cot(2𝜃_1) then would the v/v2 be the same, i cant seem to justify why?
then the ratio is apparently 3, but also not sure why.

 

[PeroK]

i mean i can treat it like a math problem, by writing down the logical conclusions:
$\tan{\alpha}=\tan{\left(\dfrac{\pi}{2}-2\theta_1\right)}-\cot{2\theta_1}$

That doesn't look right. $\alpha$ is directly related to $2\theta$.

 

[DifferentialGalois]

That doesn't look right. $\alpha$ is directly related to $2\theta$.

IT LITERALLY IS AS IT SAYS.

 

[erobz]

IT LITERALLY IS AS IT SAYS.

I wouldn't recommend "shouting" at the people trying to help you...It's impolite.

You have the following equation(s):

$$\alpha_i + 2 \theta_i = \frac{\pi}{2}$$

The value of $\theta_i$ is fixed for each car. What is $\alpha_i$ in terms of $v,v_i$ for a particular car?

 

[Steve4Physics]

Hi @DifferentialGalois. For the moment, forget about the original problem. Can you answer this...

A hailstone is falling vertically downwards at speed $v$ relative to the ground

You are driving (on the ground, straight and horizontally) at speed $u$ relative to the ground (and the hailstone's trajectory is directly in front of you).

In your (the car’s) frame of reference the hailstone appears to be moving at angle $\alpha$ to the vertical.

Can you find a formula for $\alpha$ in terms of $u$ and $v$?

Edit: Ha! @erobz beat me too it.

 

[haruspex]

IT LITERALLY IS AS IT SAYS.

@PeroK means more directly than in your equation in post #19. It does not need to involve any trig functions. How you got that is mysterious, and it cannot be right since it reduces to $\tan(\alpha)=0$. Please post your steps.