Faraday's law of electromagnetism

[Nimbus2000]

I have a confusion regarding Faraday's law of electromagnetism. Consider this diagram

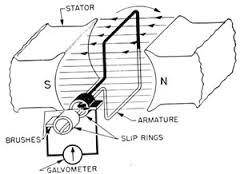
At this instant, the velocity of the rotor is parallel to the field lines, hence, no emf is induced in the rotor. Altetnatively, we can say that the rate of change of flux associated with the rotor is 0 at this instant, hence emf induced is 0.
Also, motional emf is given as E=BlvsinΘ and magnetic flux Φ=BAcosΘ. Now, E=BlvsinΘ=Bl(dx/dt)sinΘ=d(B*l*dx*sinΘ)/dt=d(BAcosΘ)/dt=dΦ/dt. This shows that if we use motional emf formula or the dΦ/dt formula, we arrive at the same result. But what if the conductor is not cutting any magnetic field and there is a change in flux with respect to the loop?

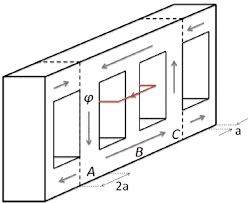
Suppose the middle limb is excited using a dc voltage. All the flux will be enclosed in the limb. Now consider the red loop on the middle limb. If the loop is tilted by some angle, flux through the loop will change since Θ changed. But the loop doesn't cut any flux since all the flux is enclosed in the limb. Will there be emf induced in the loop without cutting of flux lines?
Please help.

 

[Hesch]

Suppose the middle limb is excited using a dc voltage. All the flux will be enclosed in the limb.

A small amount of flux will be present outside the limb.

Say that the loop is just a little wider than the limb ( so that a tilt is possible ), and that the relative permeabilty, μ_r = 1000 as for the limb, the flux density just outside the limb will become 0.001*( density inside the limb ). So tilting the loop will cut a small amount of flux, and will induce a small amount of emf.

So just to be very accurate: An emf will be induced due to some flux lines being cut.

( Emf = dψ / dt , ψ = flux )

 

[Simon Bridge]

But what if the conductor is not cutting any magnetic field and there is a change in flux with respect to the loop?

... ie if all the flux is enclosed within the loop ...

In practice this won't happen.
Mathematically we can set up anything - so set up the math and crunch the numbers.

Define a uniform magnetic field in rectangular coords: $\vec B = B\hat k : -a/2 < x,y < a/2$ but 0 everywhere else, and there is a square conducting loop with sides length b > a in the x-y plane, centered on the origin. You want to rotate the loop through angle $\theta$ about the y axis, being careful to keep in bounds: $0 < \theta < \cos^{-1}(a/b)$ (check?) so that the wire never cuts the magnetic field.

You want to know if there is a change in flux due to the component of $\vec B$ perpendicular to the area of the loop changing.
Is this what you are thinking of?

The equation you want is:
$$\Phi = \iint_S \vec B\cdot \text{d}\vec S$$

It needn't be that complicated: a simple situation is to change the magnetic field strength so $\vec B = B(t)\hat k$ and leave the loop in the x-y plane. Now what happens? Is flux cutting happening?

 

[cnh1995]

... ie if all the flux is enclosed within the loop ...

In practice this won't happen.
Mathematically we can set up anything - so set up the math and crunch the numbers.

Define a uniform magnetic field in rectangular coords: $\vec B = B\hat k : -a/2 < x,y < a/2$ but 0 everywhere else, and there is a square conducting loop with sides length b > a in the x-y plane, centered on the origin. You want to rotate the loop through angle $\theta$ about the y axis, being careful to keep in bounds: $0 < \theta < \cos^{-1}(a/b)$ (check?) so that the wire never cuts the magnetic field.

You want to know if there is a change in flux due to the component of $\vec B$ perpendicular to the area of the loop changing.
Is this what you are thinking of?

The equation you want is:
$$\Phi = \iint_S \vec B\cdot \text{d}\vec S$$

It needn't be that complicated: a simple situation is to change the magnetic field strength so $\vec B = B(t)\hat k$ and leave the loop in the x-y plane. Now what happens? Is flux cutting happening?

A small amount of flux will be present outside the limb.

Say that the loop is just a little wider than the limb ( so that a tilt is possible ), and that the relative permeabilty, μ_r = 1000 as for the limb, the flux density just outside the limb will become 0.001*( density inside the limb ). So tilting the loop will cut a small amount of flux, and will induce a small amount of emf.

So just to be very accurate: An emf will be induced due to some flux lines being cut.

( Emf = dψ / dt , ψ = flux )

Thank you @Hesch, @Simon Bridge for your replies. Actually, Nimbus2000 is my friend (and room-mate) and I was facing some technical problems while posting my own thread
https://www.physicsforums.com/threads/faradays-law-confusion.882312/.
So, he posted this thread and a few minutes later I posted my own. Later, I posted another thread in which I've asked the actual question in my mind. Please have a look and see if you can help.
https://www.physicsforums.com/threads/faradays-law-and-motional-emf-paradox.882572/.