Faraday's law and motional EMF paradox

[Charles Link]

..only when the loop is stationary and the flux is varying w.r.t. time, just like in a transformer. Here, the conductor loop is moving in a stationary field and has a linear velocity v. The vxB force on the electrons of the conductor is responsible for creating the emf in such cases (which is called "motional emf"). I have posted a link in #8 about the same. Motional emf and dΦ/dt are always equal as @Dale has said earlier because when you change the flux by "moving the conductor", you "cut the field lines" . Here, emf is induced by the vxB force and mathematically, it turns out that motional emf and dΦ/dt are equal. Hence, in general we can say induced emf=rate of change of flux but the physical reasons are different when the "circuit moves in a steady field" and when the "flux varies in a fixed circuit".

Ok..Here's a quick description of the diagram..

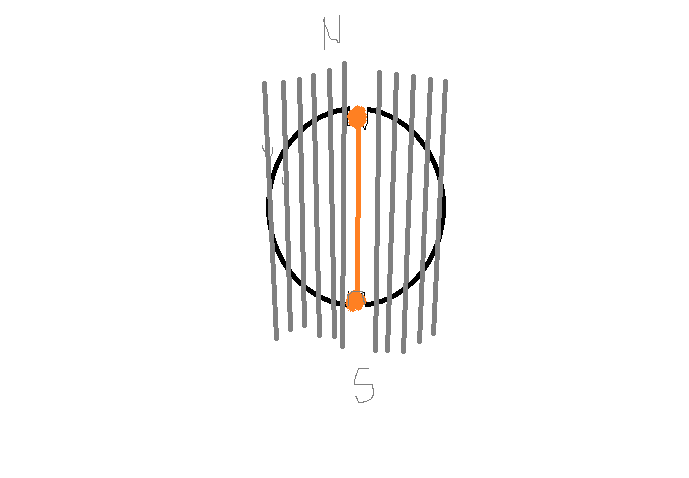
The conductor (orange) is made of copper (high reluctance) and the rest of the core is made of iron(highly permeable, negligible reluctance). Now, if the magnetic poles are created as shown (using electromagnet), most of the field lines (grey) will bypass the conductor since it has a very high reluctance, and will be crowded in the rest of the core. So, magnetic field B at the site of the conductor(orange circles) is very weak.

Isn't the B field at the site of the conductor(orange circles) much weaker than that in the rest of the core?

Your more detailed description was very helpful. Near the poles of a cylindrical magnet or horseshoe shaped magnet (i.e. in the air outside of the material), the magnetic field outside the magnet can be nearly as large as it is inside the iron core of the magnet.

 

[Charles Link]

Additional comment on this one: There is a modified version of Faraday's law that applies when the surface of interest is also changing in size. Alternatively, the effect can be viewed as due to the magnetic field acting on the moving electrons in the conductor. Both methods give the same force, but in one case it is due to an electric field and the other case due to a magnetic field. Relativistically, I think the two go hand-in-hand and are part of the electromagnetic tensor. @vanhees71 I would welcome your input here-I think this problem is similar to a paper of yours that you referenced in a recent discussion of the effects of a changing magnetic field on the circuit equations. Your paper discussed the modified Faraday's law in the case of a changing boundary surface.

 

[Dale]

Isn't the B field at the site of the conductor(orange circles) much weaker than that in the rest of the core?

Is the conductor just a straight wire through the core or is it a loop? What is the difference between the orange circles and the rest of the conductor?

Whatever the geometry of the conductor, it is possible to make the field there much lower than the field nearby.

 

[Dale]

@vanhees71 I would welcome your input here-I think this problem is similar to a paper of yours that you referenced in a recent discussion of the effects of a changing magnetic field on the circuit equations. Your paper discussed the modified Faraday's law in the case of a changing boundary surface.

I am not sure if this is the @vanhees71 post you are thinking of, but I found it useful

https://www.physicsforums.com/threads/maxwells-curl-equations.831561/#post-5223098

 

[cnh1995]

Is the conductor just a straight wire through the core or is it a loop?

It is a loop. The diagram is the front view of a cylindrical iron rotor with a single turn of conductor (two orange circles are two slots).

Whatever the geometry of the conductor, it is possible to make the field there much lower than the field nearby.

Yes. The field at the site of the conductor is much weaker than the field nearby. How is vxB emf still equal to dΦ/dt?

 

[Dale]

It is a loop. The diagram is the front view of a cylindrical iron rotor with a single turn of conductor (two orange circles are two slots).

So it is a rectangular loop? Two sides on the faces of the cylinder and two sides parallel to the axis of the cylinder?

The field at the site of the conductor is much weaker than the field nearby. How is vxB emf still equal to dΦ/dt?

What changes? What is the v and the dΦ/dt? I don't know what final state you think it is changing to.

 

[Charles Link]

It is a loop. The diagram is the front view of a cylindrical iron rotor with a single turn of conductor (two orange circles are two slots).

Yes. The field at the site of the conductor is much weaker than the field nearby. How is vxB emf still equal to dΦ/dt?

See the link that @Dale provided in post #34 to answer this question. I think it provides a very good answer. Meanwhile, additional comment is that the $v \times B$ is part of the EMF, as described in the "link", but it appears that this portion of the EMF, if I am interpreting it correctly, is not an electric field. In any case, I found the "link" quite interesting.

 

[my2cts]

"The physical reasons are different."
Only the observer reference frame is different.
In both cases there is a force given by q(E+vxB).

 

[cnh1995]

So it is a rectangular loop? Two sides on the faces of the cylinder and two sides parallel to the axis of the cylinder?

Yes.

What changes? What is the v and the dΦ/dt? I don't know what final state you think it is changing to.

The loop is initially vertical and contains zero flux. Now, if the rotor body is rotated through 90 degrees, the loop becomes horizontal and contains all the flux. This change in flux is quite large and hence, dΦ/dt is large. During the rotation of the rotor, the conductor loop will have an angular velocity ω and linear velocity v=rω, where r is the radius of the cylindrical rotor. Hence, motional emf Blv is induced in the conductor loop due to the vxB force on the electrons of the conductor.
As per Faraday's law, motional emf Blv should be equal to dΦ/dt but since the B field at the site of the conductor is much weaker than the field nearby, motional emf Blv is also very small, while dΦ/dt is very large.
I want to know how motional emf=dΦ/dt in this case? First of all, is it correct to say "motional emf is always equal to the rate of change of flux"?
If anything is still unclear from my wording, please tell me (English is not my native language). I'll try to upload a clearer diagram.

 

[cnh1995]

In any case, I found the "link" quite interesting.

It is indeed interesting..
But it's going to take me a while to digest all the math in that article as I'm not so good at vector calculus...

 

[Dale]

Thanks for the clarification. I now understand your proposed scenario.

but since the B field at the site of the conductor is much weaker than the field nearby

That is no longer true as it rotates.

First of all, is it correct to say "motional emf is always equal to the rate of change of flux"?

Yes, see the derivation I linked to earlier in the Wiki article

 

[cnh1995]

That is no longer true as it rotates.

So as the loop rotates, the B field at the site of the conductor is not weak? Doesn't the high reluctance of the conductor affect the field when the loop is rotating? Does the conductor exclude field lines only when it is at rest and cut all the field lines while it is moving?

 

[Dale]

Doesn't the high reluctance of the conductor affect the field when the loop is rotating?

Certainly it "affects it", but "affects it" is not the same as "makes it always negligible".

Reluctance isn't magic. It is the magnetic equivalent of resistance. You can still get current through a large resistor.

Does the conductor exclude field lines only when it is at rest?

If you like to use the field lines concept then it should be obvious that the only way for field lines to go from outside to inside the loop is for them to cut across the loop. During that time the B field at the loop is not negligible.

 

[cnh1995]

During that time the B field at the loop is not negligible.

Thanks for the explanation!
Just a couple of questions for confirmation..
So when the conductor is rotating, it is first cutting the field lines as they can't move from inside to outside without being cut, right? Hence, can I say that the conductor cuts all the field lines while rotating as if it didn't have a high reluctance and hence the vxB force is strong enough such that motional emf is equal to dΦ/dt?

 

[Dale]

The rest seems fine except...

as if it didn't have a high reluctance

I wouldn't go that far. It has a high reluctance, but that doesn't mean that there is never any situation where it has a magnetic field going through it.

Similarly, if a resistor has a high resistance, you can still get current through it, but you wouldn't claim that it was as if it didn't have a high resistance.

 

[cnh1995]

Thank you very much for your time @Dale!
You've been really great! This question was bugging me for a very long time and I think I've got a satisfactory answer now.
Thanks a lot @Simon Bridge, @Charles Link for your help!.

 

[Simon Bridge]

Wel done and no worries.