sciwizeh
- 25
- 0
As usual I'm working on a program and I'm having trouble with math/efficiency.
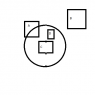
I need a way to find out if a circle given as a point and a radius C(x,y,r) fully encloses a rectangle given by the top left corner and the width and height R(x,y,w,h)
I only need to know IF it fully covers the rectangle and not any of the areas.
2. The attempt at a solution
The only solution I can think of is simple but not fast:
1) get all points of the rectangle (xi,yi) i from 1-4
2) for every i check if (cx-xi)2+(cy-xi)2 <= cr2
3) if any of the checks in 2 are false it is not covered by the circle otherwise it does
I am sure that this solution will work, but I'm hoping there may be a faster way to do it. Is this the best (most efficient) solution or is there a better one?
Homework Statement
I need a way to find out if a circle given as a point and a radius C(x,y,r) fully encloses a rectangle given by the top left corner and the width and height R(x,y,w,h)
I only need to know IF it fully covers the rectangle and not any of the areas.
2. The attempt at a solution
The only solution I can think of is simple but not fast:
1) get all points of the rectangle (xi,yi) i from 1-4
2) for every i check if (cx-xi)2+(cy-xi)2 <= cr2
3) if any of the checks in 2 are false it is not covered by the circle otherwise it does
I am sure that this solution will work, but I'm hoping there may be a faster way to do it. Is this the best (most efficient) solution or is there a better one?