Feynman diagrams for ##e^{+}e^{-}\rightarrow \mu^{+}\mu^{-}##

[spaghetti3451]

Consider the process of electron-positron annihilation into muons as given by

$$e^{+}e^{-}\rightarrow \mu^{+}\mu^{-}.$$

The Feynman diagrams for this process to lowest-order are given by

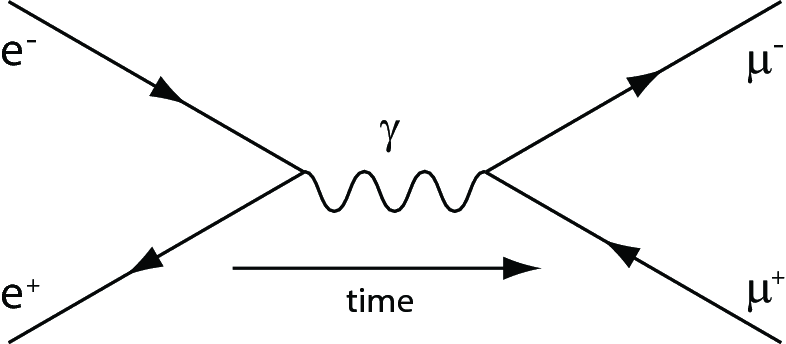
This is an s-channel diagram.Why are there no t-channel or u-channel diagrams for this process?

 

[vanhees71]

Well, try to draw $t$- and $u$-channel diagrams for QED. You'll see that they contradict the Feynman rules, because within QED flavor is conserved!

 

[spaghetti3451]

I see!

Can you explain this using the interaction term in the Lagrangian that describes this process?

 

[vanhees71]

The interaction terms read
$$\mathcal{L}_{\text{int}}=e (\overline{\psi}_e \gamma^{\mu} \psi_e + \overline{\psi}_{\mu} \gamma^{\mu} \psi_{\mu}) A_{\mu}.$$
Now find the Feynman rules for the vertices and compare them to what you'd need to be allowed to draw $t$- and $u$-channel Feynman diagrams for pair annihilation.

 

[spaghetti3451]

The interaction terms read
$$\mathcal{L}_{\text{int}}=e (\overline{\psi}_e \gamma^{\mu} \psi_e + \overline{\psi}_{\mu} \gamma^{\mu} \psi_{\mu}) A_{\mu}.$$
Now find the Feynman rules for the vertices and compare them to what you'd need to be allowed to draw $t$- and $u$-channel Feynman diagrams for pair annihilation.

Got it, thanks!

 

[hilbert2]

This thread made a related question come to my mind, and it's probably not necessary to start another thread for it... Is there some fundamental reason why two Dirac fermion fields are always coupled only through some intermediate bosonic field, and can't have a direct coupling? I.e. why can't there be an interaction term proportional to something like $\overline{\psi_\mu}\psi_e$ ? I know that the answer is probably something very simple, like that this would not be compatible with unitary time evolution or special relativity, but I'm an applied physicist by specialty, so it isn't immediately obvious to me.

 

[vanhees71]

You "can't have" such a coupling because of lepton conservation. It's an empirical input to the Standard Model.

 

[hilbert2]

You "can't have" such a coupling because of lepton conservation. It's an empirical input to the Standard Model.

Thanks for the answer. I looked this up at Google and I only found vague mentions of four-fermion interactions happening in some effective field theories: https://en.wikipedia.org/wiki/Four-fermion_interactions

Maybe there's some way to combine the electron, positron, muon and antimuon fields in some term in a way that conserves net lepton numbers. Something like $\overline{\psi}_{\mu} \psi_{e} \overline{\psi}_{e} \psi_{\mu}$ ... But of course, no one has ever observed such interactions so I'm just playing with the math here.

 

[vanhees71]

You get such interactions in effective field theories by contracting the internal boson lines, if there is, e.g., a large mass in the corresponding propagator (as for the W and Z bosons). Then you get something like Fermi's theory of beta decay as an effective theory with (non-renormalizable) four-fermion couplings.

 

[Vanadium 50]

Hilbert, what you wrote down corresponds to an electron bopping along and suddenly becoming a muon. Violates conservation of energy.

 

[hilbert2]

^ Ok. I didn't bother to try to expand those point interaction terms with creation and annihilation operators. Obviously the interaction should only be able to turn an electron-positron pair with large kinetic energy to a muon-antimuon pair. Isn't the $\overline{\psi}_{\mu} \psi_{e} \overline{\psi}_{e} \psi_{\mu}$ a bit similar to the phi-4 interaction for a single scalar field?