- #1
Sekonda
- 201
- 0
Hey again,
I have a question on a couple of things related to feynman diagrams but also the relativistic scalar propagator term.
First of all, this interaction:
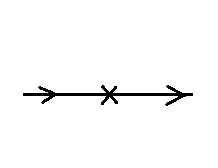
The cross represents a self-interaction via the mass and characterised by the term: -im^2, is this just some initial state then self-interacting with itself via the mass, with nothing changing and it entering into a final state the same as the initial state? Can anybody explain what exactly is happening in this interaction?
My second question is on the propagator for a relativisitc scalar particle, I believe it has form:
\frac{i}{E^{2}-\mathbf{p}^{2}-m^{2}}
My professor said that this is where this form comes from, he said to imagine summing up all the possible number of self-interaction from 0 self interactions to (presumably) and infinite number of interactions, so :
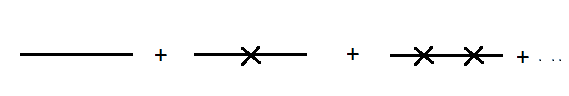
So the first line has no mass interaction so m=0 and the factor for the first one is :
\frac{i}{E^{2}-\mathbf{p}^{2}}
then the second line has one mass interaction so the factor associated with it is :
\frac{i}{E^{2}-\mathbf{p}^{2}}(-im^{2})\frac{i}{E^{2}-\mathbf{p}^{2}}
and the third line has 2 mass interactions and so the factor is :
(\frac{i}{E^{2}-\mathbf{p}^{2}})^3(-im^{2})^2
And so we sum all these factors up (to the maximum number of self-interactions) and can make factorisation below:
\frac{i}{E^{2}-\mathbf{p}^{2}}(1+\frac{m^{2}}{E^{2}-\mathbf{p}^{2}}+\frac{m^{4}}{(E^{2}-\mathbf{p}^{2})^2}+\cdots )
We use identity:
(1+x)^{-1}=1+x+x^{2}+x^{3}+\cdots\: ,\: x=\frac{m^{2}}{E^{2}-\mathbf{p}^{2}}
and thus obtain the relativistic scalar propagator:
\frac{i}{E^{2}-\mathbf{p}^{2}-m^{2}}
How does this work? Is the scalar interaction just the sum of all the self-interactions by mass?
Thanks,
SK
I have a question on a couple of things related to feynman diagrams but also the relativistic scalar propagator term.
First of all, this interaction:
The cross represents a self-interaction via the mass and characterised by the term: -im^2, is this just some initial state then self-interacting with itself via the mass, with nothing changing and it entering into a final state the same as the initial state? Can anybody explain what exactly is happening in this interaction?
My second question is on the propagator for a relativisitc scalar particle, I believe it has form:
\frac{i}{E^{2}-\mathbf{p}^{2}-m^{2}}
My professor said that this is where this form comes from, he said to imagine summing up all the possible number of self-interaction from 0 self interactions to (presumably) and infinite number of interactions, so :
So the first line has no mass interaction so m=0 and the factor for the first one is :
\frac{i}{E^{2}-\mathbf{p}^{2}}
then the second line has one mass interaction so the factor associated with it is :
\frac{i}{E^{2}-\mathbf{p}^{2}}(-im^{2})\frac{i}{E^{2}-\mathbf{p}^{2}}
and the third line has 2 mass interactions and so the factor is :
(\frac{i}{E^{2}-\mathbf{p}^{2}})^3(-im^{2})^2
And so we sum all these factors up (to the maximum number of self-interactions) and can make factorisation below:
\frac{i}{E^{2}-\mathbf{p}^{2}}(1+\frac{m^{2}}{E^{2}-\mathbf{p}^{2}}+\frac{m^{4}}{(E^{2}-\mathbf{p}^{2})^2}+\cdots )
We use identity:
(1+x)^{-1}=1+x+x^{2}+x^{3}+\cdots\: ,\: x=\frac{m^{2}}{E^{2}-\mathbf{p}^{2}}
and thus obtain the relativistic scalar propagator:
\frac{i}{E^{2}-\mathbf{p}^{2}-m^{2}}
How does this work? Is the scalar interaction just the sum of all the self-interactions by mass?
Thanks,
SK