Field momentum inside a parallel plate capacitor

[brian0918]

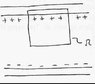
The system is a parallel plate capacitor, top plate has charge density sigma, bottom play has charge density -sigma. I'm looking for the "field momentum" inside the cubic volume Omega shown in the picture.

My book (Griffiths) is a little unclear on exactly what this is, and seems to be saying that the momentum is proportional to the Poynting vector ExB, so since there doesn't seem to be a magnetic field, this would suggest the field momentum is zero.

Is this correct?


The only problem I'm having is that, later in the problem, it asks if there's a net flow of field momentum into the cube, so I'm thinking there's more to the problem than what I'm seeing. Could anyone help clear this up?


Thanks.

 

[Tide]

Unless you have current flowing through the dielectric or it's part of an AC circuit you won't have a magnetic field. Is there any other information provided?

 

[brian0918]

There's no other information. So the field momentum is indeed zero?

What about a net flow of the field momentum into the cubic volume Omega?

 

[Tide]

There's no other information. So the field momentum is indeed zero?

What about a net flow of the field momentum into the cubic volume Omega?

That would imply an infinite buildup of momentum/energy over time not to mention there is no source for that.

 

[brian0918]

Are you sure about the net flow into volume Omega being zero? If you look at the picture, the volume doesn't include the negative plate, just the positive plate. Does this change anything? The book doesn't explain this at all.