- #1
PainterGuy
- 940
- 69
Hi!
Could you please help me with the queries below? Thanks a lot.
Question 1:
My question is about the field outside the plates of parallel plate capacitor. It is said that the field(s) between positively and negatively charged plates gets added up but the field(s) outside the plates gets canceled up. I don't understand how the external field(s) could get canceled up.
Please have a look on this Figure #1 below.
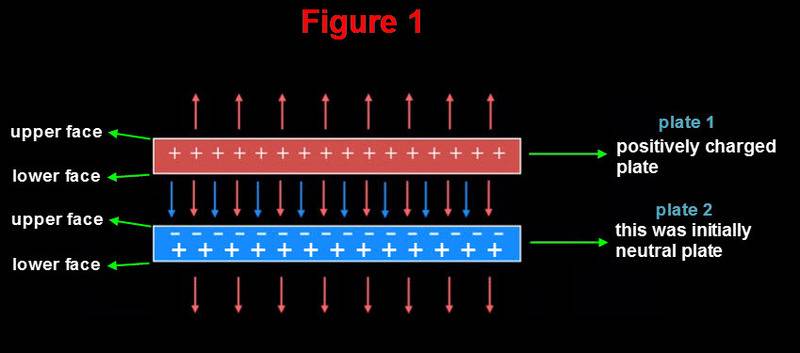
In the figure above plate 1 is positively charged and plate 2 was initially neutral. As plate 2 is exposed to the field of positively charged plate, the charge in it gets redistributed and one side of it becomes negatively charged and the other side becomes positively charged. We should note that number of 'positive' field lines emanating from the lower face of plate 2 is equal to the number of positive field lines entering upper face. Also, the both plates are electrically neutral between their upper and lower faces/boundaries. By the way, I believe that in a positively charged plate, plate 1, the charges would also redistribute in a way that the upper face would be less positively charged compared to the other one. I hope you agree with me up to this point.
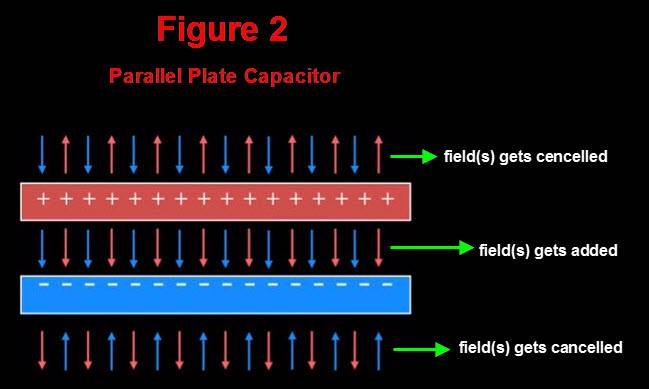
Now please have a look on Figure #2 below. It shows how electric field of parallel plate capacitor is shown at many places though I don't agree that the field could get canceled outside.
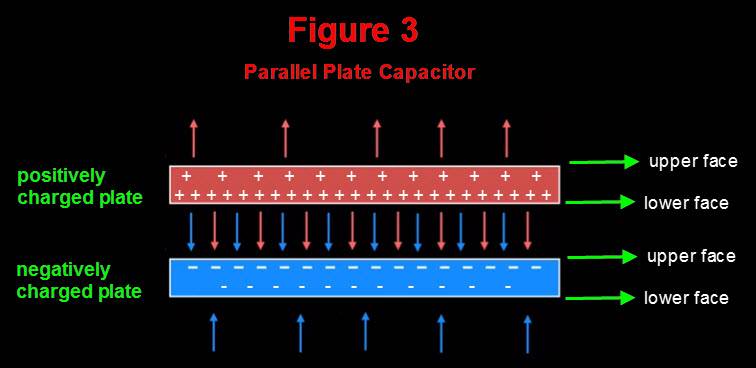
In Figure #3 below I'm trying to show how in my opinion charges get redistributed once both positively and negatively charged plates are brought close together. I cannot understand how fields could get canceled toward the upper face of positively charged plate and toward the lower face of negatively charged plate. Where am I going wrong?
Question 2:
Electric for a parallel plate is given as shown below.
E=Q/(ε0A) where ε0 is vacuum permittivity and A is area of the plates
E=Vab/d where Vab is potential difference between the plates and 'd' is distance between them
I don't understand how reducing the distance between plates increases electric field. If the charge and area of plates don't change, 'd' shouldn't matter. It's not that reducing the 'd' would affect the charge, Q. Could you please guide me with this?
You could watch the video between 6:09 - 6:21. That section shows how 'd' affects electric field.
applet used in the video: https://phet.colorado.edu/en/simulation/capacitor-lab
Thank you!
Could you please help me with the queries below? Thanks a lot.
Question 1:
My question is about the field outside the plates of parallel plate capacitor. It is said that the field(s) between positively and negatively charged plates gets added up but the field(s) outside the plates gets canceled up. I don't understand how the external field(s) could get canceled up.
Please have a look on this Figure #1 below.
In the figure above plate 1 is positively charged and plate 2 was initially neutral. As plate 2 is exposed to the field of positively charged plate, the charge in it gets redistributed and one side of it becomes negatively charged and the other side becomes positively charged. We should note that number of 'positive' field lines emanating from the lower face of plate 2 is equal to the number of positive field lines entering upper face. Also, the both plates are electrically neutral between their upper and lower faces/boundaries. By the way, I believe that in a positively charged plate, plate 1, the charges would also redistribute in a way that the upper face would be less positively charged compared to the other one. I hope you agree with me up to this point.
Now please have a look on Figure #2 below. It shows how electric field of parallel plate capacitor is shown at many places though I don't agree that the field could get canceled outside.
In Figure #3 below I'm trying to show how in my opinion charges get redistributed once both positively and negatively charged plates are brought close together. I cannot understand how fields could get canceled toward the upper face of positively charged plate and toward the lower face of negatively charged plate. Where am I going wrong?
Question 2:
Electric for a parallel plate is given as shown below.
E=Q/(ε0A) where ε0 is vacuum permittivity and A is area of the plates
E=Vab/d where Vab is potential difference between the plates and 'd' is distance between them
I don't understand how reducing the distance between plates increases electric field. If the charge and area of plates don't change, 'd' shouldn't matter. It's not that reducing the 'd' would affect the charge, Q. Could you please guide me with this?
You could watch the video between 6:09 - 6:21. That section shows how 'd' affects electric field.
applet used in the video: https://phet.colorado.edu/en/simulation/capacitor-lab
Thank you!
