Figuring out when to use the two different voltage equations

[cookiemnstr510]

Homework Statement

I have two problems, both using different equations for electric potential. Confused on when to use which.
First problem:
Two parallel plates connected by a battery whose electric potential is 12V. One plate Has charge density σ⁺ and the other has Charge density σ⁺. The plates are spaced 3x10^-3m. We want to find the electric field. The way the problem is solved:
ΔV=U/q
U=qEd
Combining the two above:
ΔV=Ed→E=ΔV/d→E=12V/(3x10^-3m)=4x10³V

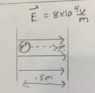
The next problem wants to know the electric potential energy of moving a proton like the attached picture.
It is solved like this:
ΔV=-Ed=-(8x10⁴V/m)(0.5m)=-4x10⁴V
Then:
ΔU=qΔV=(1.602x10^-19C)(-4x10⁴V)=-6.4x10^-15J

My question:
Why I’m the first problem did we say ΔV=Ed
And in the second problem
ΔV=-Ed?
Thanks!

 

[kuruman]

The Greek letter Δ stands for "change" of the quantity that follows. Change is defined as final value minus initial value, what comes later minus what comes earlier. Electric field lines always point from a region of high potential V to a region of low potential V. So, if you move with the field lines, the change is negative and if you move against the field lines, the change is positive.

In the first question you are given the "voltage" or electric potential difference across the battery terminals. This is conventionally chosen as positive. In this problem there is no movement of charges from one terminal to the other as is the case in the second problem.

 

[cookiemnstr510]

The Greek letter Δ stands for "change" of the quantity that follows. Change is defined as final value minus initial value, what comes later minus what comes earlier. Electric field lines always point from a region of high potential V to a region of low potential V. So, if you move with the field lines, the change is negative and if you move against the field lines, the change is positive.

In the first question you are given the "voltage" or electric potential difference across the battery terminals. This is conventionally chosen as positive. In this problem there is no movement of charges from one terminal to the other as is the case in the second problem.

Thank you! I didn’t know that about electric field lines.